Ciências da computação dia 67

Na última aula de sistema digitais, vimos como era possível utilizar flip-flops e alguns outros componentes para criar um circuito que seguia uma certa sequência de valores. Agora, vamos ver um pouco sobre circuito que podem reconhecer padrões em cadeias de bits.

Digamos que você queira reconhecer dentre vários bits, uma sequência de exatamente 3 zeros.

Podemos pensar nesse problema da seguinte forma.

Imagine que a entrada será essa sequência de bits

1110010000000000111111010101010100010001000010001

Com a sequência de entrada em mãos podemos começar a encontrar os padrões e adicionar 1 para se a sequência for a que queremos e 0 se não for

1110010000000000111111010101010100010001000010001

0000000010010010000000000000000000100010001000010

Com essa sequência podemos começar a pensar como o circuito poderá ser montado.

Como vamos utilizar flip-flops, precisamos pensar como vamos armazenar a contagem. Da maneira mais simples que podemos pensar, podemos contar, em decimal mesmo, quantos zeros achamos, resultando em uma sequência semelhante a esta:

1110010000000000111111010101010100010001000010001

0000000010010010000000000000000000100010001000010

0001201231231231000000101010101012301230123101230

Criando esta sequência mais amigável, vamos começar a criação do nosso grafo dirigido.

O grafo dirigido

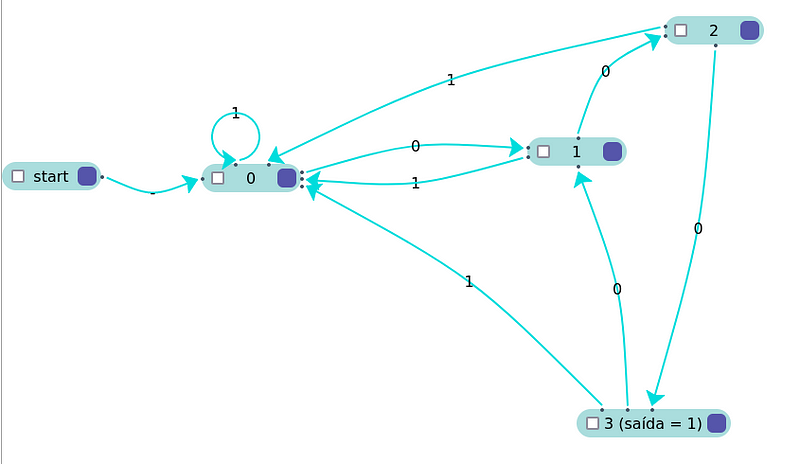
O grafo que está logo acima, possui 4 estados (0--3), cada um deles representa a quantidade de zeros encontrados. Se começarmos com a sequência e o primeiro valor for 1, ocorrerá um enlace e o valor continuará em 0, caso contrário, será contabilizado um valor zero no próximo estado (1). Estando no valor 1, se o próximo valor for 1, ele voltará para o 0, limpando a contagem, caso contrário será contabilizado mais um valor 0 (estado 2). Estando no estado 2, se o próximo valor for um número 1, a contagem será reiniciada, caso contrário mais um valor 0 será contabilizado (estado 3) e a saída será um número 1, já que encontramos uma sequência de 3 zeros. Estando com 3 zeros contabilizados, se o próximo número for um a contagem se reiniciará, se não será contabilizado 1 valor 0 (estado 1).

Quantidade de flip-flops necessários

com o grafo completo, podemos começar a pensar no circuito, mas antes precisamos pensar quantos flip-flops serão necessários para fazê-lo.

Seguindo a regra de 2^x ≥ QE (onde x é a quantidade de flip-flops e QE a quantidade de estados do grafo).

Plugamos os valores

2^x ≥ 4

2^x ≥ 4

o menor valor para x que satisfaz a inequação é 2, sendo assim precisamos de 2 flip-flops.

Montando a tabela de estímulos

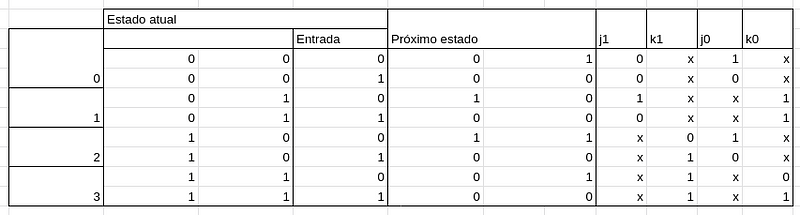
Diferente da tabela de estímulos que montamos na aula passada, esta vai ter uma peculiaridade a mais. Desta vez precisamos saber qual a entrada que receberemos.

Mapas de Karnaugh

Para montarmos os mapas de Karnaugh entramos em um dilema, como colocaremos os valores?

Repare que na tabela de estímulos, os valores dos estados atuais forma uma sequencia perfeita de 000 até 111 em binário, sendo assim podemos pegar essas sequencias e dizer que a primeira linha dos estados é referente ao 0, a segunda ao 1, e assim por diante.

Com isso, podemos pegar esses valores referentes a cada linha para achar a localização no mapa de Karnaugh (nesse caso de duas variáveis).

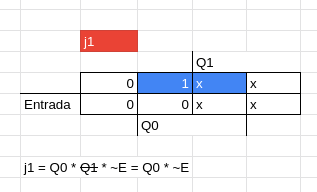
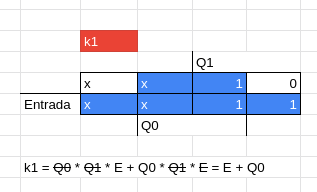
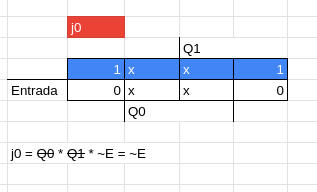
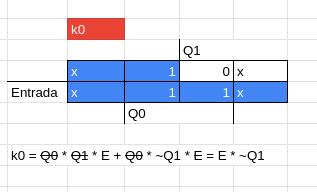
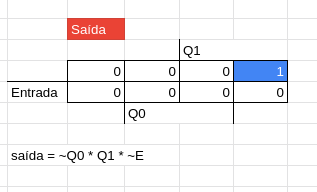
Montando o Circuito

Com tudo pronto, podemos começar a montar o circuito, resultando em algo semelhante a isso:

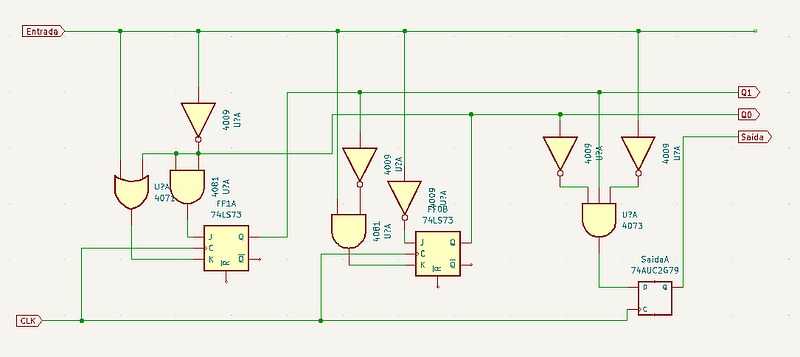
Repare que para a saída usamos um flip-flop do tipo D. De maneira resumida, usamos ele pois além de não possuir aquelas saídas inválidas (já que dentro possui um flip-flop JK) ele ainda deixa a saída igual a sua entrada, além de possuir apenas uma entrada e uma saída que para o nosso propósito faz todo sentido.