Ciências da computação dia 65

• Um determinante é um número resultante de uma matriz quadrada;
• Pode ser representado como: |A| ou det(A);
• Podem também ajudar a resolver sistemas de equações.

O determinante de uma matriz 2x2 pode ser calculado da seguinte forma

|A| = a11 * a22 --- a21 * a12

exemplo:

| 2 3 |

| 4 5 |

|A| = 2 * 5--4 * 3 = 10--12 = -2

em inequações:

| 2 x |

| 4 5 |

| A | ≤ 0

2*5 --- x*4 ≤ 0

10--4x ≤ 0

-4x ≤ -10

x ≤ -10/-4

x ≤ 5

em inequações de segundo grau:

A

| x 2 |

| 5 x+1|

B

| 5 -x |

| -1 x |

| A | ≥ | B |

x(x+1) --- 10 ≥ 5x --- x

x² + x --- 10 ≥ 4x

x² --- 3x --- 10 ≥ 0

a = 1; b = -3; c = -10

Δ = b² --- 4ac

Δ = (-3)² --- 4 * 1 * (-10)

Δ = 9 + 40 = 49

-b +- √Δ / 2a

3 +- 7 / 2

3 + 7 / 2 = 5

3--7 / 2 = -2

como sabemos que o a da inequação é > 0 então sambem que a concavidade do gráfico ficará para cima.

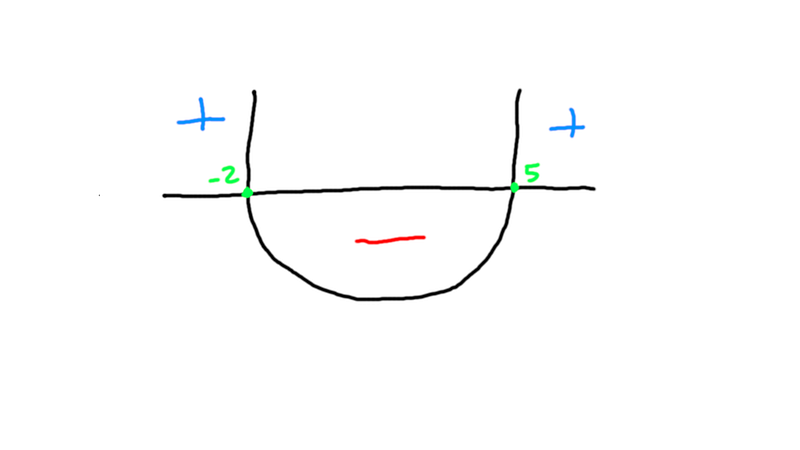
como sabemos queremos os valores que resultaram em um resultado ≥ 0, então precisamos pegar todos que são positivos e que resultam em zero, sendo assim, podemos pegar todos os elementos até -2 e depois todos os elementos depois de 5

Notas

toda vez que você fizer uma operação entre um elemento e seu inverso, você sempre encontrará o elemento nulo daquela operação, exemplos:

1 + (-1) = 0

A * A^-1 = I