Ciências da computação dia 48
Finalização Distribuição Normal
Bem, no artigo do dia 45 comecei a falar sobre distribuição normal. No entanto ainda faltaram alguns detalhes.
Digamos que você queira calcular a área que está na beira do gráfico, para isso faça 50-x dessa forma:
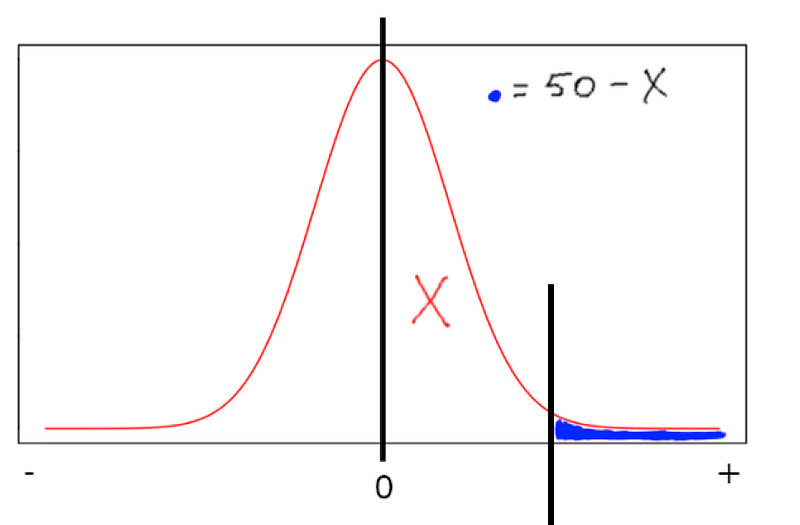
Lembrando que a formula de z antes descrita calcula do zero até o resultado, então x sempre será do zero para frente/trás.
Agora digamos que você queira calcular o valor que está entre outros dois valores, digamos P(7 < x < 10)
para você fazer isso faça
- calcule um z para cada um dos dois valores (7 e 10)
2. coloque eles no grafico
3. veja como esses dados esta no grafico
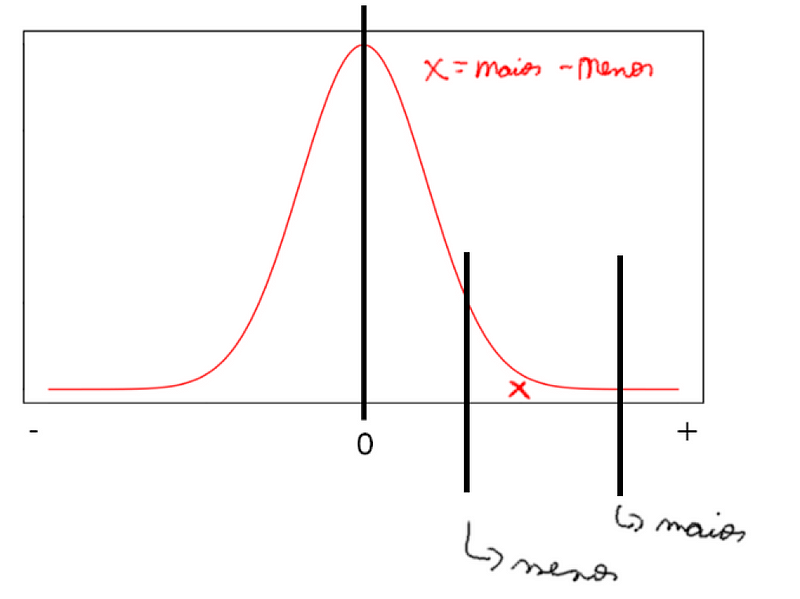
a. Se eles estiverem do mesmo lado faça (área do maior valor --- área do menor valor):
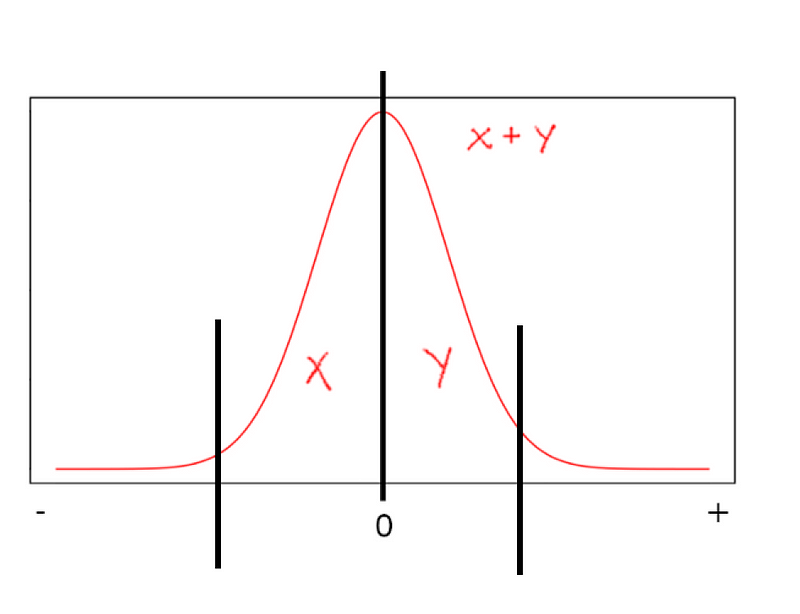
b. Se eles estiverem cada um de um lado basta somar os valores das áreas:
Por fim, digamos que você tenha um problema que quer o inverso, ele quer por exemplo saber 75% do grafico representa quanto do nosso problema. Nesse caso faça o seguinte:
Primeiramente entenda que para esses casos as porcentagens vão da esquerda para a direita de ordem crescente, com isso pintaremos os 75% da seguinte forma:
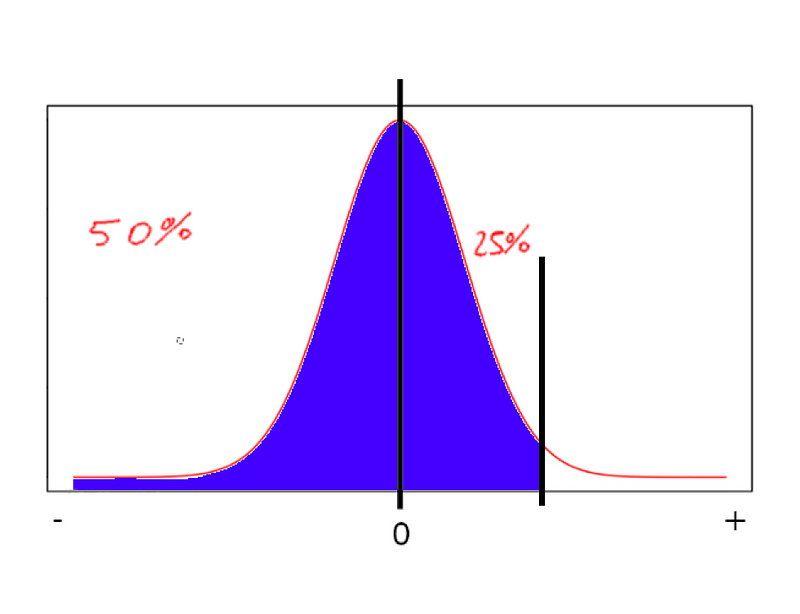
agora você pega os 25% e encontra naquela tabela a probabilidade mais proxima de 25% (ou 0,25) que não ultrapasse esse valor, após isso pegue o valor de Z correspondente.
Esses valores são:
probabilidade mais próxima: 0,2486
Z = 0,67
com esses valores você irá colocar na formula de Z:
z = (x --- x̅ ) / S
sendo que para esse exemplo:
x̅ = 8, S = 2 e Z = 0,67
então:
0,67 = (x --- 8) / 2
2*0,67 = x --- 8
1,34 = x --- 8
x = 1,34 + 8
x = 9,34 (valor que 75% representa)