Ciências da computação dia 46

Calculo de ângulos

Na escola geralmente aprendemos sobre o triângulo retângulo e junto com o teorema de Pitágoras começamos a ver sobre funções trigonométricas (seno, cosseno, tangente).

sendo assim as funções que estamos acostumados a ver são:

Sen(α) = cateto oposto / hipotenusa

Cos(α) = cateto adjacente / hipotenusa

Tg(α) = cateto oposto / cateto adjacente

No entanto, caso quiséssemos encontrar o inverso, ou seja qual ângulo possui certo valor como Tg, Sen ou Cos, teríamos que usar tabelas como as seguintes:

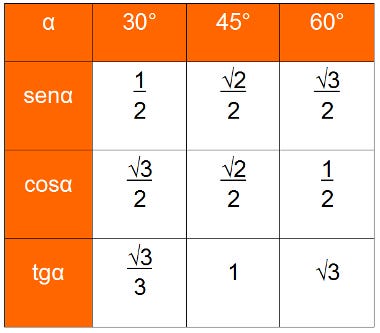
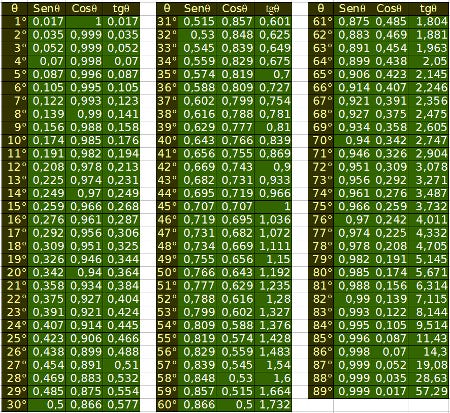
E ainda lembrar ângulos como 0, 90, 180, 270, 360, que para isso é bom se relembrar do circulo trigonométrico

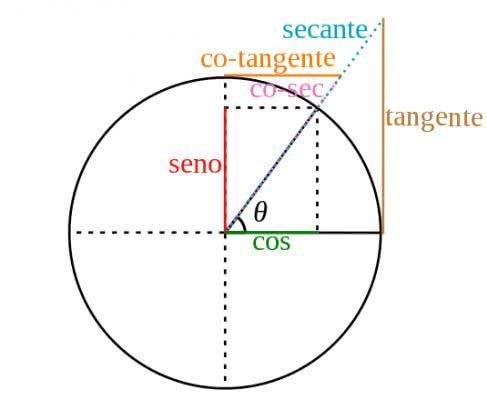
Lembrando que a tangente de 90 e 270 não existem pois esses ângulos formam retas paralelas com a reta da tangente por isso não existem. Podemos pensar nisso também se usarmos a formula tg = sen/cos, veremos também que 1/0 e -1/0 não existem

obs: essa fórmula funciona pois, a tg = cateto oposto / cateto adjacente, e a reta do seno e a reta vertical que por sua vez também representa o cateto oposto do ângulo teta, e o mesmo vale para o cosseno, a reta do cosseno e a horizontal que por sua vez também é o cateto adjacente à teta.

No entanto, para acharmos esses ângulos não precisamos usar essas tabelas, apenas usar a inversa de cada uma dessas funções (também chamado de arco dessas funções)

então se sen(30) = 1/2

então arcsen(1/2) = 30

se cos(60) = 1/2

entao arccos(1/2) = 60

se tg(45) = 1

entao arctg(1) =45

obs: essa função inversa também pode ser representada como: sen⁻¹, cos⁻¹ e tg⁻¹

Eliminação de Gauss

Como aprendemos antes, em sistemas lineares geralmente usamos o método da soma, do qual pegamos os sistemas e queremos transformar uma das incógnitas em 0, e depois terminar usando uma equação simples para achar a outra incógnita. Isso funciona perfeitamente para duas variáveis.

Já para três, esse método é mais complexo de ser feito, sendo assim é usada a regra de Cramer para resolver o sistema.

Contudo, conforme o número de variáveis vão aumentando, vai ficando cada vez mais difícil de resolver a regra de Cramer então, utilizamos a eliminação de Gauss para sistemas lineares com mais de 3 variáveis, isso não é uma regra, mas é o que geralmente é feito.

O sistema linear que estarei usando aqui é o seguinte:

x + 2y =5

2x --- 2y + 3z = 9

3x + 3y --- 2y = 3

antes de começarmos com a eliminação de Gauss, será necessário fazer a regra de Cramer para saber se o sistema terá solução. Então, para isso, faça:

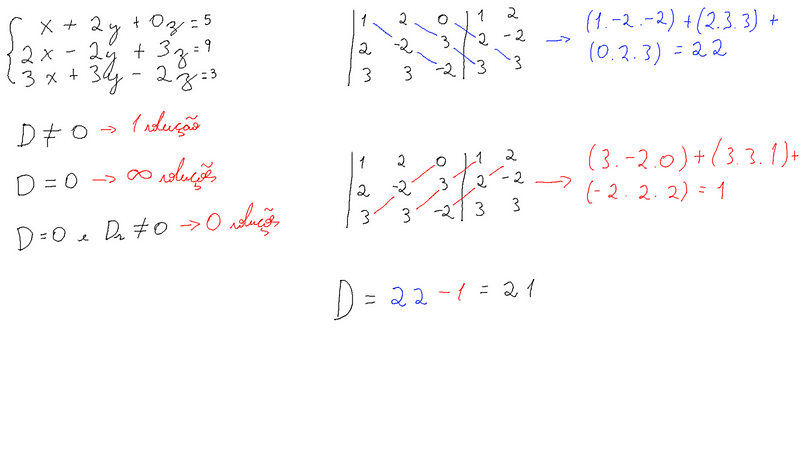
pegando os valores que acompanham as variáveis, transferindo-os para uma matriz e duplicando as primeiras duas colunas temos o esqueleto do que precisamos para resolver a regra de cramer. Com isso montado podemos pegar as diagonais principais, multiplicar os valores e somar com os outros. Após isso, fazemos o mesmo para as diagonais secundárias e por fim subtraimos o valor obtido na soma das diagonais principais pelas secundárias e obtemos o determinante (D).

Com esse valor em mãos podemos saber quantas soluções o sistema terá, como o valor foi diferente de 0, terá 1 solução e poderemos continuar com a eliminação de Gauss.

Fazendo agora a eliminação de Gauss, pegamos todos os valores do sistema e colocamos em uma matriz da seguinte forma:

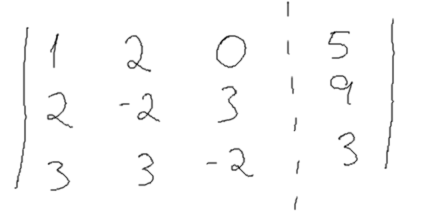
A partir de agora, devemos escolher um pivot,esse número não importará muito, mas ele será usado aqui para termos um norte. Geralmente esse número é o primeiro da matriz nesse caso o 1.

Com isso devemos analisar que equação podemos usar para fazer com que o número abaixo do pivot se transforme em zero usando apenas as operações (+,-,*)

observando um pouco podemos chegar na ideia da equação: (valor da linha 2) --- 2 * (valor da linha 1)

Isso pois ao colocar o 2 como o valor da linha 2 e como o valor da linha 1 e realizar a equação chegamos ao valor 0.

Então realizamos essa operação para todos os valores da linha dois

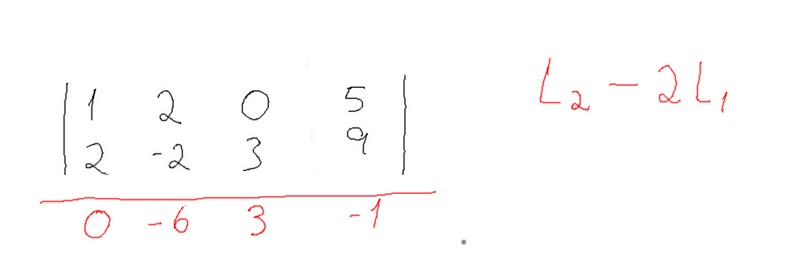
Com esses valores substituimos a linha 2

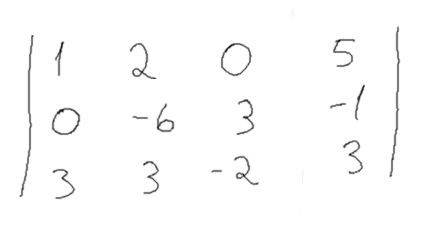
e escolhemos o novo pivot que deve ser o valor da linha + 1 e coluna + 1, nesse caso o valor -6

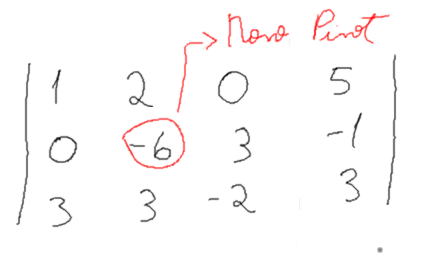
E novamente escolhemos uma equação que faça os valores abaixo e antes do pivot se tornem 0, nesse caso (L3--3*L1)

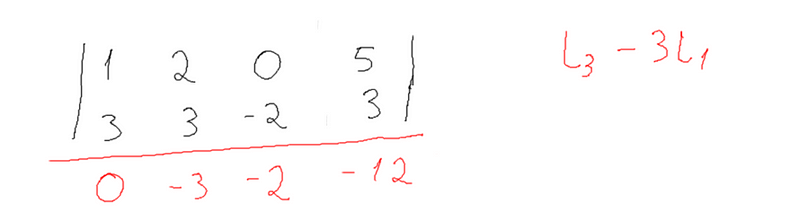
Pegamos esses valores colocamos na terceira linha e novamente vamos procurar uma equação que faça o valor em baixo do pivot se tornar zero, já que a equação feita anteriormente foi para fazer o valor antes do pivot se tornar 0. Nesse caso a equação que satisfaz é a 2 * L3 --- L2

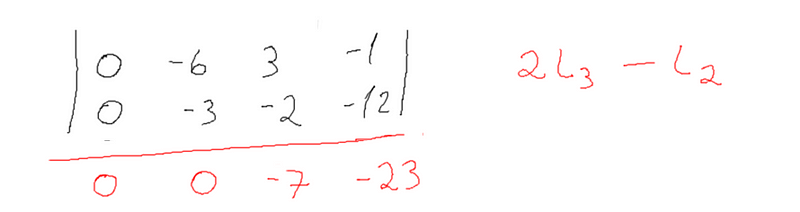
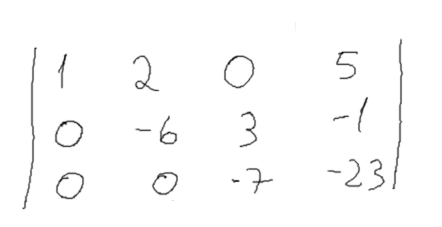
Essa é a matriz final, veja que no canto inferior esquerdo temos uma espécie de triângulo com 3 zeros, esse é o momento para parar (quando seu triângulo de zeros tiver o mesmo número de linhas).

Com essa matriz vamos encotrar os resultados.

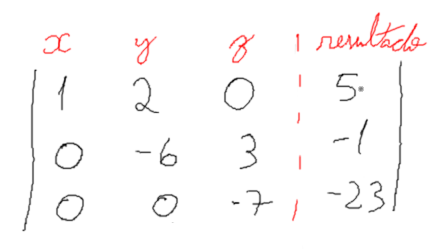
Repare que cada coluna é relativa a uma variável do sistema linear. Então podemos pegar esses valores e montar um novo sistema da seguinte forma:

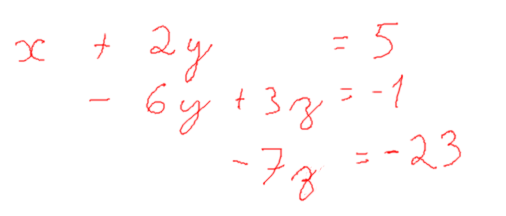
Com isso agora é so resolver!

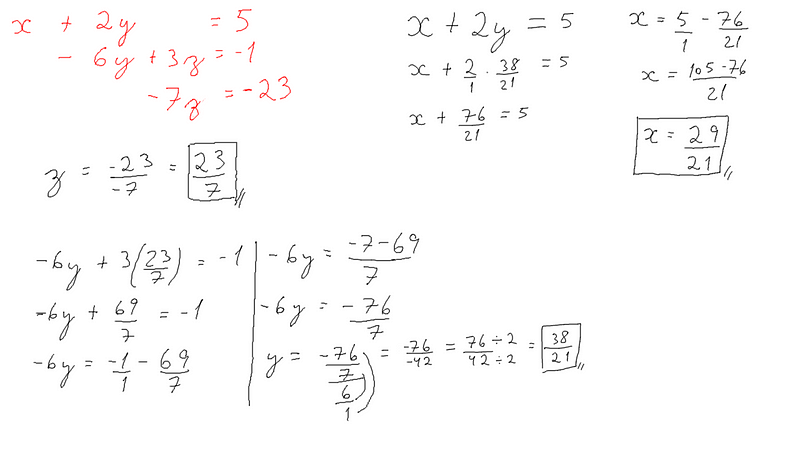
Resolvendo as equações temos que:

x = 29/21

y = 38/21

z = 23/7