Ciências da computação dia 45

créditos: andre zibetti

Distribuição normal

Nesta aula, começamos a ver sobre distribuição normal, do qual é um método utilizado para descrever probabilidades em conjuntos de espaços contínuos.

Antes de começar vamos ver alguns símbolos e termos que serão usados:

Algo não pontual → Algo que pode ser descrito de diversas maneiras para que seja verdade, exemplo: P(produzir mais de 100 quilos de farinha de trigo em uma hora), esse mais de 100 quilos, pode ser 100.01, 100.00000001, 101, etc. existem diversos valores que satisfazem esse requerimento;

Classes → Intervalos de valores/categorias que há em um conjunto de dados. Esses são dados que estão em um intervalo, ou seja seus valores não se repetem;

Frequência (fi) → Quantidade de vezes que algo aparece. No caso com classes a quantidade de vezes que os valores estão em certo intervalo;

Mediana (xi) → Valor do meio de um conjunto de dados. Como iremos usar Classes que possuem valores em um certo intervalo, não precisamos ver todos os valores pegar o do meio ou se o conjunto for par pegar os dois do meio e dividir por dois, por serem dados que não se repetem podemos usar a seguinte fórmula (primeiro valor+último valor) / 2;

Total de frequências (n) → Soma de todos os valores das frequências;

Somatório (∑) → Ferramenta matemática para representar que algo deverá ser somado, usado em conjuntos. Exemplo

x =1, 2, 3, 4, 5

∑x = 1 + 2 + 3 + 4 + 5

Média (x̅) → Demonstra a onde os dados estão concentrados. No nosso caso iremos usar a média ponderada que se dá pela seguinte equação

x̅ = (∑ xi.fi)/n

Desvio (di) → Distância que a média está da mediana. Por ser uma distância, não há a possibilidade de ser um valor negativo, por isso essa equação está contida entre um módulo(||), sendo assim a equação será: di = |xi --- x̅ |;

Desvio médio(Dm) → Média dos desvios. Como na média, o Desvio médio também é calculado usando a média ponderada da seguinte forma:

Dm = (∑ di.fi)/n

Variância(S²) → Indica o quão longe seus valores estão da média. Sua formula é a seguinte: S² = (∑ di².fi)/n --- 1.

Obs: note que S²é o símbolo da variância, ou seja, você não deverá utilizar a raiz do resultado;

Desvio Padrão(S) → Indica o quão uniforme seus dados são. Sua equação é:

S = √(S²) ← S² é a variância;

Coeficiente de Variação(Cv) →Descreve o quanto nossa média é verdadeira, ou seja se nossa média foi resultado de varias vezes o mesmo número aparecer, ou se por algum acaso outros números acabaram se juntando e dando essa média. Esse valor nunca passa de 1, e quanto menor ele for, mais verdadeira é sua média. Sua formula é:

Cv = S / x̅

valores de Cv

0 → todos os valores são os mesmos, por isso sua média foi essa

≤ 0.5 → seus valores variam, mas no geral ficam na média

> 0.5 → valores variam muito, dados completamente dispersos e oscilantes

Agora, depois desse mini resumo do que será usado para entender melhor dados, vamos ver um exemplo:

Imagine que você tenha uma tabela com os seguintes dados:

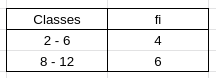
Seu objetivo aqui é encontrar o valor de Cv, sendo assim para isso iremos usar todas aquelas equações que passei anteriormente.

1 --- Encontrar os valores de xi

(2+6 )/ 2 = 4

(8+12)/2 = 10

xi = 4, 10

2 --- Fazer a média

x̅ = (∑ xi.fi)/n

valores de xi.fi →16, 60

∑ xi.fi = 76

n = 4 + 6 = 10

x̅ = 76 / 10

x̅ = 7.6

3 --- Fazer o desvio

di = |xi --- x̅ |

di = |4--7.6| → 3.6

di = |10--7.6| → 2.4

di = 3.6, 2.4

4 --- Fazer desvio o desvio médio

Dm = (∑ di.fi)/n

valores de di.fi →14.4, 14.4

∑di.fi = 28.8

Dm = 28.8 / 10

Dm = 2.88

5 --- Fazer a variância

S² = (∑ di².fi)/n --- 1.

valores di² →12.96, 5.76

valores de di².fi →51.84, 34.56

obs: aqui ao invés de você fazer primeiro os valores de di² para depois multiplicar com fi, você poderia pegar os valores de di.fi e multiplicar cada um deles pelo seu di de novo

∑ di².fi = 86.4

S² = 86.4/9

S² = 9.6

6 --- Fazendo o desvio padrão

S = √(S²)

S = *√*9.6

S = 3.09

7 --- Fazendo o coeficiente de variação

Cv = S / x̅

Cv = 3.09 / 7.6

Cv = 0.4

Pronto conseguimos encontrar o valor de Cv, mas agora você pode estar pensando, para que eu usaria isso?

Bem, você pode usar para diversas coisas que possuam dados em intervalos,e caso você queira entender melhor como todos eles se comportam, podendo ser usado por exemplo, para vendas, te mostrando como suas vendas vão indo (possuem uma certa regularidade, vende a mesma quantidade todo mês, geralmente certo mês vende mais do que outro, etc.), com avaliações, saber se todos estão te dando notas altas ou você possui tantas notas que no geral sua media fica boa, etc. Com essa ferramentas, você pode utilizar para casos como esses e ter alguns insights de como você pode agir no seu dia a dia.

No entanto, existe mais um caso que você pode acabar se deparando.

Exemplo:

A média de emails é de 80/dia, o desvio padrão é de 20, qual a probabilidade da quantidade de e-mails enviados em um dia ser >70

para isso você precisará de três coisas

1 . z = (x --- x̅ )/S

com essa formula você encontrará em qual posição do eixo X da curva de Gauss seus dados estão

fazendo com os dados acima

x = 70

x̅ = 80

S = 20

(70--80̅ )/20 → -0.5

2. Colocar z na curva de Gauss

A curva de gauss(distribuição normal)é um modelo matemático que tenta mostrar graficamente a distribuição de dados de forma que é possível notar um certo padrão em seus comportamento a partir do crescimento desses dados.

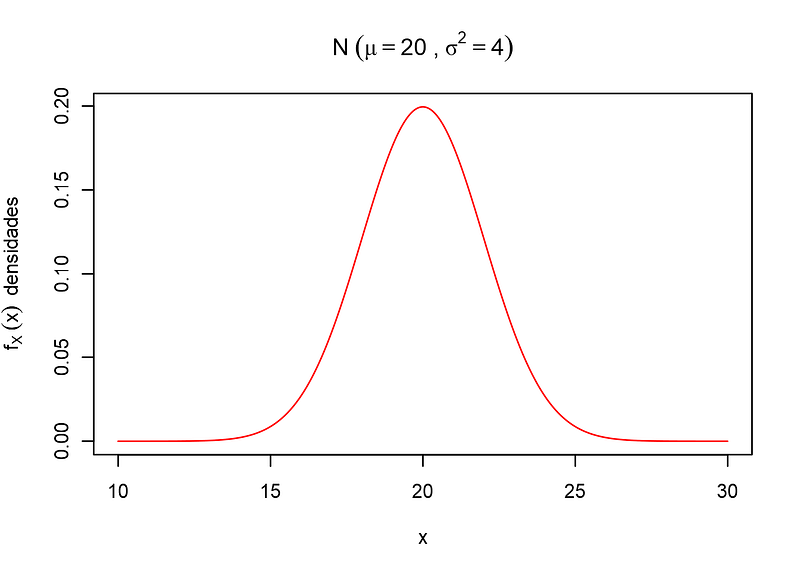
Agora faça um modelo da curva de Gauss parecido com esse:

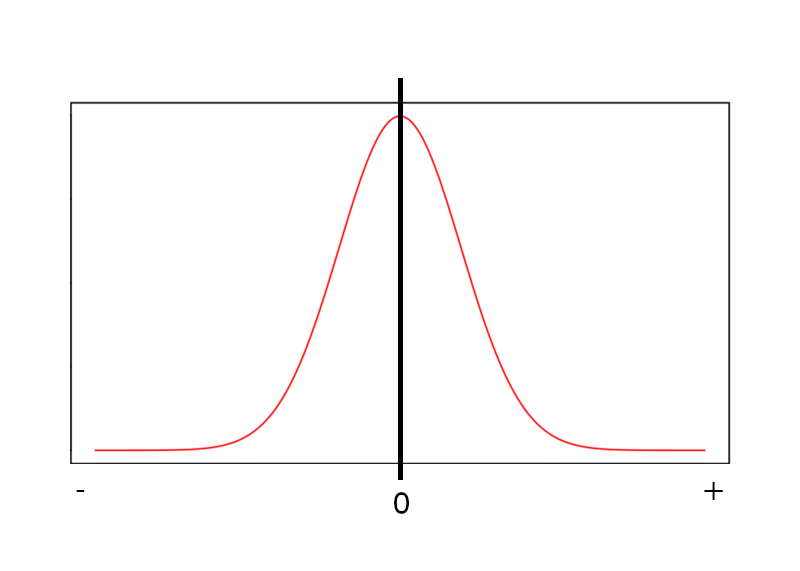
A partir disso, vamos pegar o valor que achamos para z e vamos colocar no gráfico.

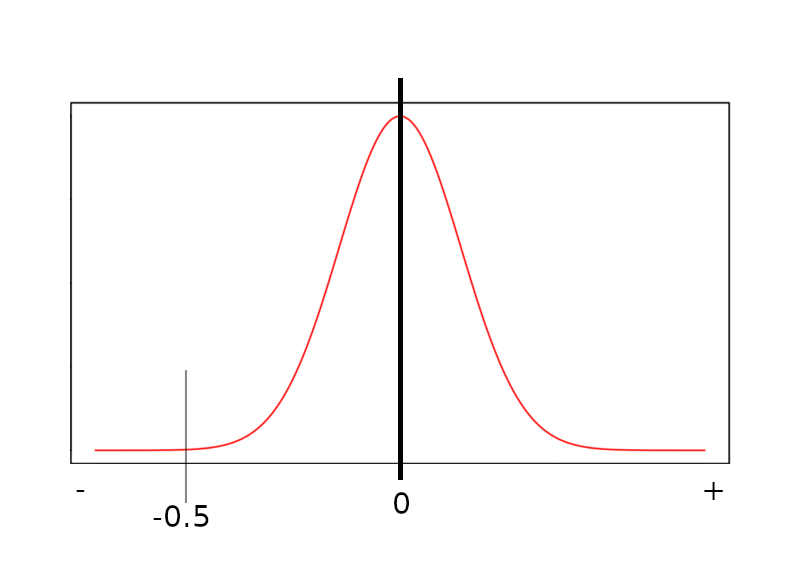
2. Encontrar a área do gráfico

Agora, com o gráfico podemos pensar algumas coisas,como queremos os valores maiores que 70, podemos pensar no símbolo do > como uma seta que aponta para a direita, sendo assim iremos pintar tudo que está adiante do ponto -0.5 do gráfico, caso fosse valores menores é só fazer o inverso

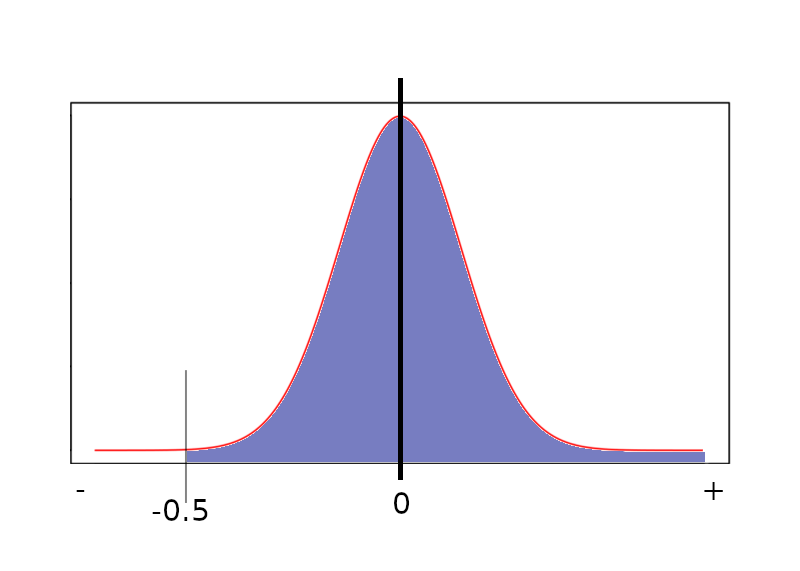
Agora podemos pensar. Se o gráfico está dividido no meio, e tudo depois do meio está pintado, então temos 50% + o valor de 0 até -0.5 em porcentagem, para encontrar esse valor é necessário uma tabela

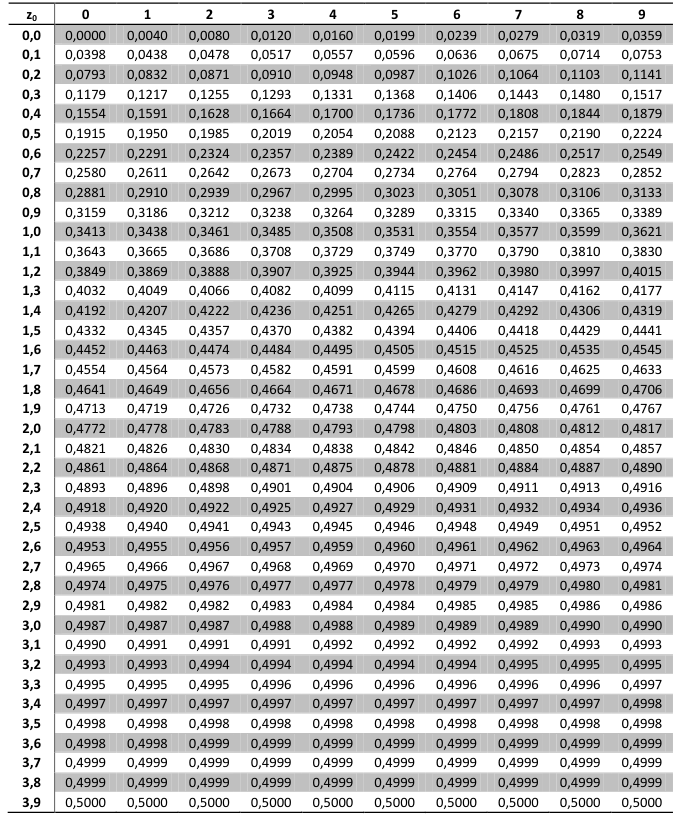
Usando essa tabela iremos até a linha do 0.5 e como a segunda casa decimal de 0.50 é 0, então pegaremos o primeiro valor (coluna 0), valor 0.1915

Agora multiplicaremos por 100 e teremos 19.15%, somando com os outros 50%, temos 69.15% de chance de a média de e-mails enviados em um dia ser >70

Observações

C6,5 = C 6,1

ou seja a combinação sempre será a mesma quando, C x,x-y = Cx, y