Ciências da computação dia 44
continuação, mapas de Karnaugh de quatro variáveis
Na ultima aula dessa matéria, começamos a ver um pouco sobre mapas de Karnaugh de quatro variáveis, que de maneira geral, é a mesma coisa do que o mapa com 3 variáveis, com apenas uma região a mais.
No entanto, na aula seguinte, aprendemos um conceito novo, do qual se denomina, termo irrelevante
Termo irrelevante
O termo irrelevante, é, como o nome já supõe, um termo em que seu valor não importa, sendo assim, podemos utiliza-lo como bem entendermos, adicionando 0 ou 1 como seu valor para deixar mais fácil nossa vida.
Geralmente, seu essa posição no mapa é representada pelo valor X, já que o valor que será atribuído será uma incógnita que nós devemos preencher da melhor maneira.
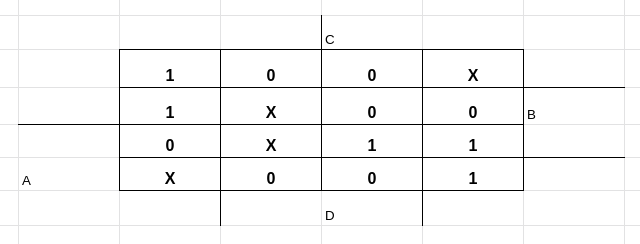
No exemplo que fiz acima, estou considerando todos os X como o valor 1 mas, caso você prefira, você pode considerar 0, use sempre aquilo que lhe fará chegar no circuito mínimo.
Agora, vamos encontrar os implicantes mas, antes disso, note uma coisa:
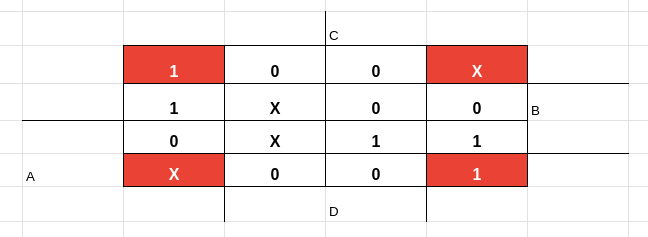
Esses quatro cantos também são um implicante, uma vez que podemos fazer o seguinte:
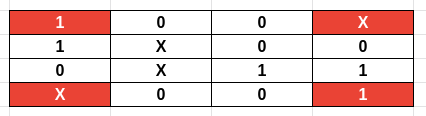
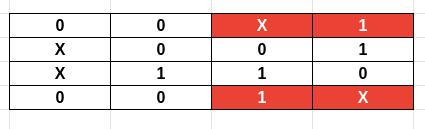
Fazendo isso, podemos juntar as colunas que estão em cima com as de baixo e fazer um implicante maior com quatro células.
A partir disso, podemos ver todos os implicantes que estão nesse mapa, contudo há mais duas regras para os termos irrelevantes.
1 --- Não pode haver um implicante composto apenas por termos irrelevantes, ou seja:
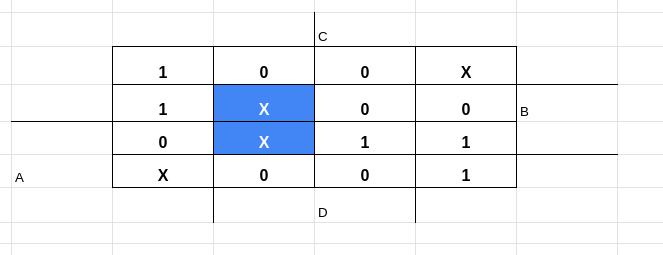
Esse implicante acima não é válido!
2 --- Um implicante em que as células que o fariam ser um implicante essencial (célula em que nenhum outro implicante sobrepõe) são termos irrelevantes, o transformam em um implicante não essencial. Ou seja:
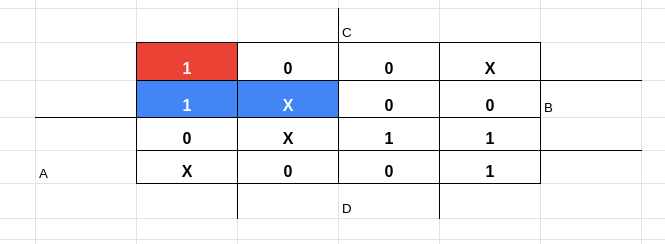
O implicante em azul, possui uma célula que não está sendo tomada por outro implicante (o implicante vermelho pega os dois valores 1, célula 0 e 4). No entanto, o valor desta célula é X, sendo assim esse implicante será não essencial.
Após entender essas regras, o resto é completamente igual ao que já foi feito anteriormente, basta pegar todos os implicantes, separa-los entre essenciais e não essenciais, fazer as expressões lógicas e pronto.
Por fim, você pode acabar encontrando expressões lógicas que lhe passam as células que possuem valores irrelevantes como neste exemplo:
f(a,b,c,d) = Π(1,3,6,7,9,11,12) * Πx(2,5,8,13)
Nesse exemplo, estamos usando o produtório (símbolo Π ou ainda π), ou seja, todas essas linhas terão o valor 0, mas note que há um termo multiplicado Πx(2,5,8,13) , esse termo representa os valores irrelevantes, sendo assim nas células 1,3,6,7,9,11,12 você colocará o valor 0, e em 2,5,8,13 a letra X.
Observações
Geralmente implicantes primos possuem no máximo 2⁴ células, ou seja 16 valores, há a possibilidade de maiores, mas dificilmente será necessário, pois o mapa se tornaria muito grande e difícil de trabalhar.