Ciências da computação dia 36

Para criarmos um somador de binário com portas lógicas precisaremos de dois circuitos, um para a soma em si e outro para o carry bit(também chamado de vai 1)

para isso, faremos uma tabela verdade com todas as possibilidades de carry bit e de somas

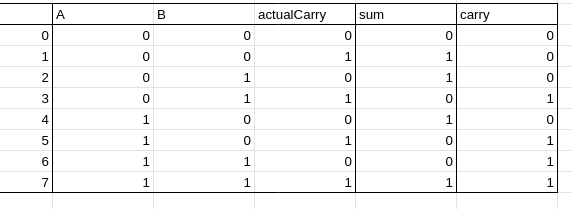
repare que o actualCarry é o valor que será somado junto com A e B, e o carry é quando na ultima soma o resultado excede a base e seria necessário mais um bit para colocar o valor na frente

ex:

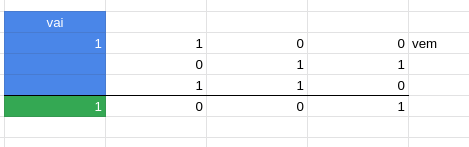
observe que, quando não é excedida a base o valor do vem é 0, e quando na ultima soma, (A + B + actualCarry) nesse caso o valor excede a base, resultando em 10, ou seja o 0 fica em baixo e sobe 1, no entanto estávamos somando 3 bits, e agora com esse carry precisaremos de mais 1, sendo assim o circuito do carry será responsavel por esse ultimo digito

no entanto note uma coisa

A e B esta duplicado

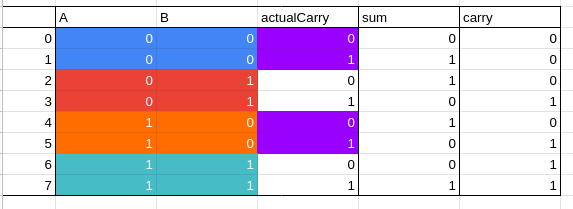
agora observe que o actualCarry ele sempre segue essa ordem, sendo assim, temos todas as combinações possíveis com 2 bits, levando em conta tbm o carry bit

agora, para conseguirmos o circuito podemos fazer o mapa de karnaugh para a coluna sum e carry, no entanto, o sum não é necessário já que existe uma porta lógica que já faz a soma em binário, denominada de XOR(exclusive or), então para essa vamos apenas associar portas XOR entre as entradas A, B e actualCarry

ficando algo assim:

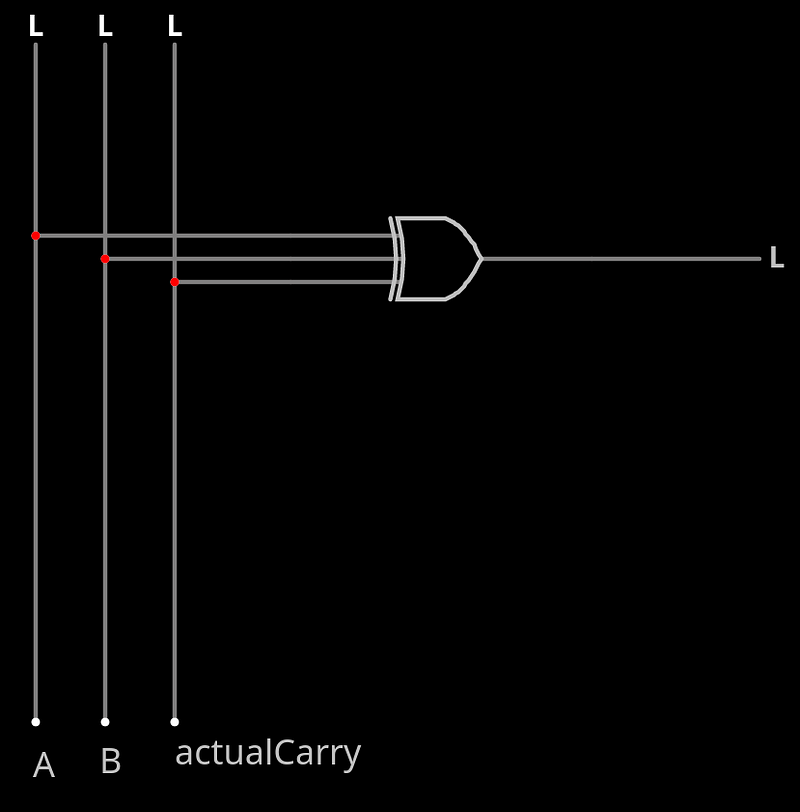
Agora pegando o circuito do carry com o mapa de karnaugh, temos

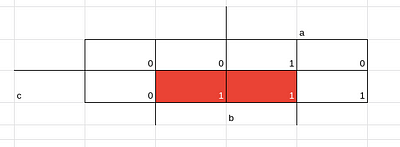
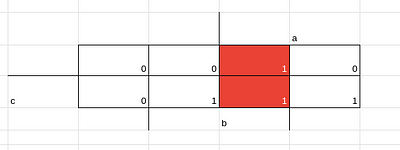
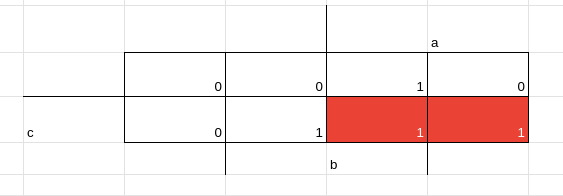
pegando os três implicantes e fazendo a soma de produtos temos:

f(a,b,c) = b.c +a.b + a.c

obs:o 'c' nesse caso é o actualCarry

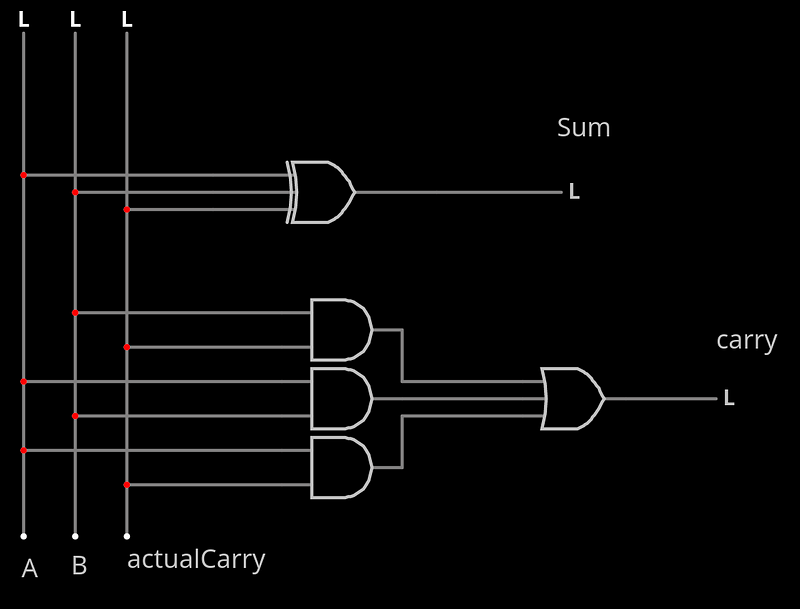
agora temos nosso somador completo de 2 bits

como observação deixo aqui que é possível interligarmos vários desses para termos somas maiores, basta você ligar o carry resultante de um no actualCarry no seguinte