Ciências da computação dia 34

Implicantes não essenciais

no artigo passado sobre esse mesmo tema, dei uma breve explicação do que serião implicantes não essenciais, mas agora vamos um pouco mais a fundo neles

os implicantes nãos essenciais, são implicantes que todos os 1 são cobertos por outros implicantes

Implicantes essenciais

o implicante essencial é aquele em que pelo uma célula pertence a apenas esse implicante

obs: quando falo que pertence a um implicante, lembre-se sempre de que pensamos em pegar os maiores implicantes possíveis, já que se fôssemos pegar de 1 em 1 todos serão essenciais

como achar implicantes essenciais e não essenciais

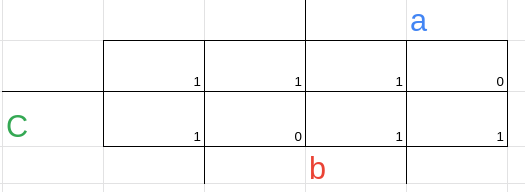
1 --- encontre todos os implicantes possíveis

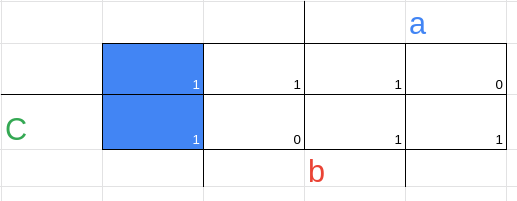
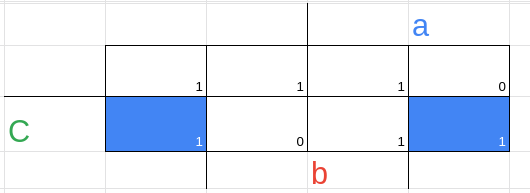
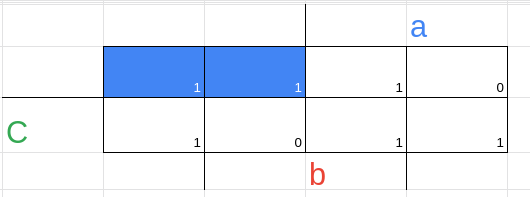
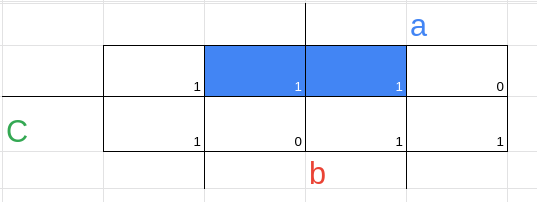
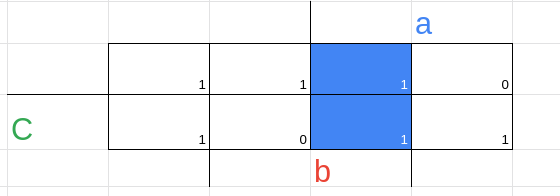
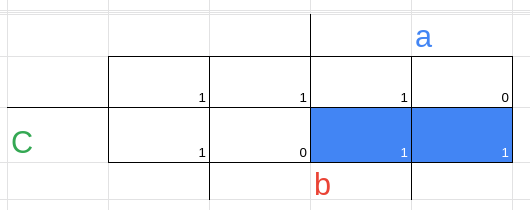
2 --- vemos quais são essenciais e não essenciais

Essenciais

Nenhum

Não essenciais

Todos

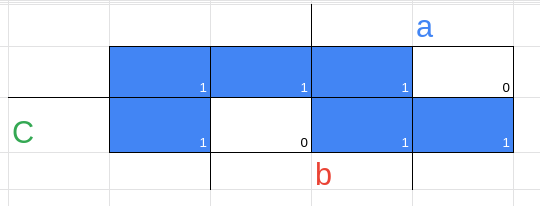
(0, 1) = a'.b'.c → a'.b'

(1, 5) = a.b'.c → b.c'

(0,2) = a'.b.c' → a'.c'

(2,6) = a.b.c' → b.c'

(6,7) = a.b.c → a.b

(5,7) = a.b.c → a.c

3 --- Veja quais são as expressões que podemos usar para cobrir todos os 1

obs: se tivesse algum implicante essencial ele sempre apareceria nas expressões (de preferência sempre no começo); Além disso, poderíamos ter colocado também todos os não essenciais, o resultado seria o mesmo, mas o circuito ficaria inviável por isso pegamos apenas aqueles que são de fato necessários

Possíveis expressões úteis

f1(a,b,c) = a'.b' + b.c' + a.c

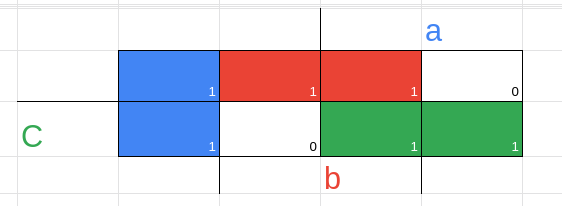
f2(a,b,c) = b'.c + a'.c' + a.b

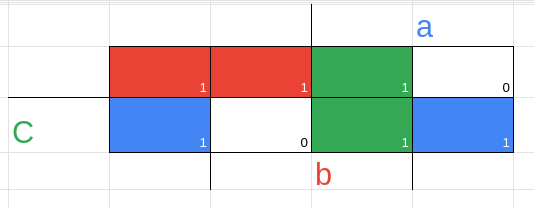
obs: claramente existem vários outros possíveis resultados, mas aqui estamos sempre pensando em os menores circuitos, então esses satisfazem nosso requerimento

Exemplo com implicante essencial junto

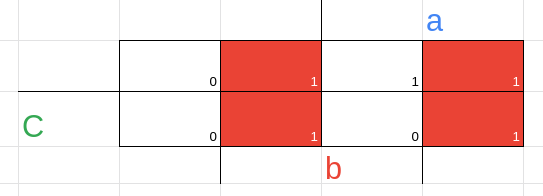
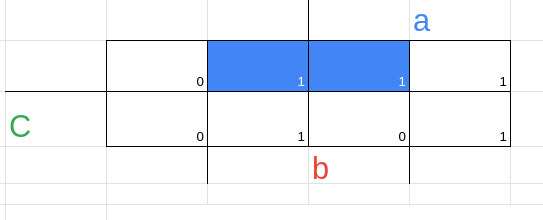
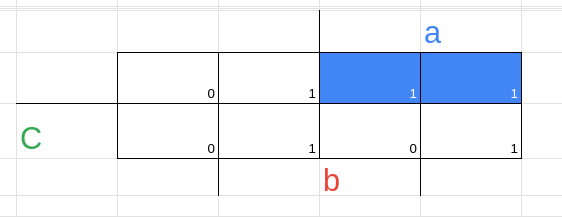
temos aqui, dois implicantes essenciais em vermelho

e dois implicantes não essenciais em azul

sendo assim temos:

Essenciais

(2,3) = a'.b.c →a'.b

(4,5) = a.b'.c →a.b'

Não essenciais

(2,6) = a.b.c' →b.c'

(4,6) = a.b.c' →a.c'

agora pegaremos todos os essenciais, e os não essenciais que podem participar para tapar todos os 1

f1(a,b,c) = a'.b + a.b' + b.c'

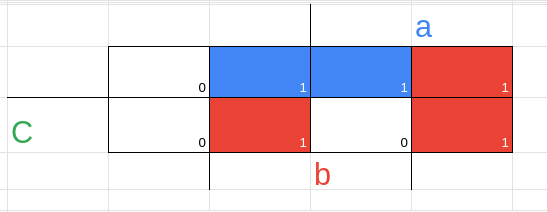
f2(a,b,c) = a'.b + a.b' + a.c'

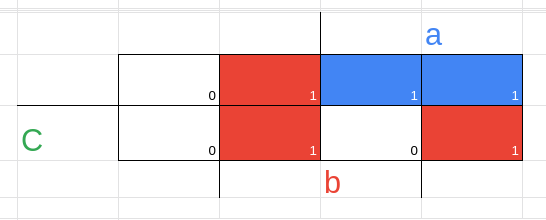
Observações

Σ → sigma e o nome do símbolo → ele representa o somatório antes explicado