Ciências da computação dia 32

Bom, no último artigo que fiz sobre simplificação de expressões e circuitos, disse sobre o mapa de karnaugh, mas tem um detalhe que nos foi explicado só na ultima aula que foi: quando nós barramos (negamos, complementamos) uma variável na expressão final?

para isso devemos entender algumas coisas:

quando um implicante primo esta totalmente em uma região → a variável referente a essa região ficará em sua forma padrão na expressão final

quando um implicante primo tem uma parte dentro e uma parte fora → essa variável será removida da expressão

quando um implicante está totalmente fora de uma região → essa variável será negada

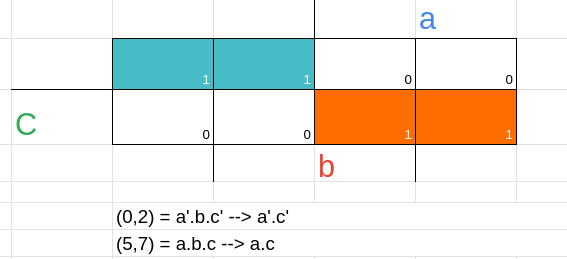
Utilizando produto de somas

nos mapas de Karnaugh utilizar soma de produtos não é uma regra

caso você queira pegar o produto de somas, basta pegar os 0 ao invés dos 1 e usar no final + ao invés de *

sendo assim a equação final será → f(a,b,c) = a+c' * a' + c que é a mesma coisa que f(a,b,c) = a'.c' + a.c

Mapas com implicantes maiores

Nos mapas de Karnaugh devemos sempre pegar os maiores implicantes possíveis, pois isso ajuda a diminuir o circuito. Isso não é uma regra, mas como queremos diminuir nosso circuito/expressão caso isso não seja feito, resultará em um circuito maior

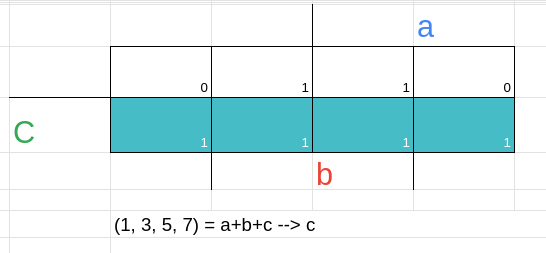
sendo assim o resultado é f(a,b,c) = b+c

lembrando que o maximo de implicantes que você pode pegar de uma vez são dados através de potências de dois sendo assim nesse caso como temos apenas 3 variaveis o maximo que conseguimos pegar é 2³ = 8

mas também poderiamos pegar

2⁰ = 1

2¹ = 2

2² = 4

2³ =8

Implicantes Essenciais

até agora vimos implicantes em diversos exemplos, e todos eles possuem uma mesma característica

todos eles são implicantes essenciais, ou seja só conseguimos montar de uma maneira os implicantes de forma que todos os números 1 apareçam

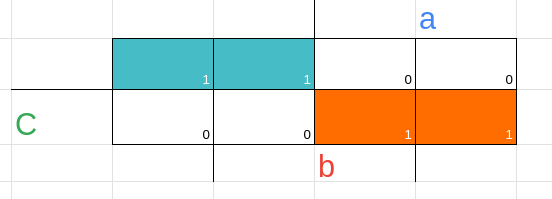
nesse mapa, por exemplo, não há como juntarmos os 1 de maneiras diferentes, ou seja todos os implicantes que conseguimos juntar são essenciais

Observações

o maxtermo é associado ao + pois a operação OR só se tornará 0 quando todos os elementos forem 0, e o mesmo acontece com os mintermos, são associados ao * pois a operação AND só será 1 quando todas as variáveis forem 1.

os implicantes primos também podem ser chamados de cobertura(s),sendo assim, nenhum valor pode ser ficado para traz (nesse caso os números 1), desde um único numero sozinho ou com mais vizinhos, ou seja devemos cobrir (fazer uma cobertura) em todos os números que nos interessam