Ciências da computação dia 30

Representação de funções lógicas

até agora representamos uma função lógica com tabela verdade, expressões matemáticas e circuitos lógicos, vamos agora ver mais algumas maneiras de se representar uma função lógica.

formas canônicas

• soma de produtos
• produto de somas

nessas duas representações temos os conceitos de maxtermos e mintermos

maxtermos → linhas de uma tabela verdade das quais o resultado é 0

mintermos → linhas de uma tabela verdade das quais o resultado é 1

soma de produtos

adicione uma AND (*) entre as variáveis para todos os mintermos, depois faça adicione negado onde for necessário para o resultado desse AND ser 1

exemplo tabela da porta OR

x y

0 0 → 0

0 1 → 1 → x * y → x' * y

1 0 →1 → x * y → x * y'

1 1 → 1 → x * y → x * y

agora pegue as expressões que resultaram e junte-as com uma operação or

f(x,y) = (x' * y) + (x * y') + (x * y)

essa é a expressão final

lembrando que você também pode usar os axiomas para reduzi-la

produto de somas

adicione uma OR (+) entre as variáveis para todos os maxtermos, depois faça adicione negado onde for necessário para o resultado desse OR ser 0

exemplo tabela da porta AND

x y

0 0 → 0 → x + y → x + y

0 1 → 0 → x + y → x + y'

1 0 →0 → x + y → x' + y

1 1 → 1

agora pegue essas expressões e junte-as com uma porta AND

f(x, y) = (x + y) * (x + y') *(x' + y)

essa é a expressão resultante e você também pode reduzi-la usando os axiomas

Somatório

o somatório é uma técnica da qual você armazena a informação de quais linhas possuem maxtermos

exemplo tabela AND

i | x y

0 | 0 0 → 0

1 | 0 1 → 0

2 | 1 0 →0

3 | 1 1 → 1

obs: o i nesse caso está representando o numero da linha

sendo assim o somatório dessa função é:

f(x, y) = Σ(0, 1, 2)

dessa forma quando você for montar a tabela verdade, você preenche tudo usando aquela técnica de numero de linhas / 2, numero de linhas /2.... e na hora de adicionar os resultados com o somatório você já sabe quais os resultados serão 0

Produtório

O produtório tem uma ideia semelhante a do somatório, mas nesse caso você fará para os mintermos

exemplo tabela OR

i | x y

0 | 0 0 → 0

1 | 0 1 → 1

2 | 1 0 →1

3 | 1 1 → 1

sendo assim o produtório disso é:

f(x, y) = π(1, 2, 3)

o mesmo pode ser usado para saber quais linhas vão ter o valor 1 na hora de montar a tabela verdade

Mapas de Karnaugh

• forma de simplificar um circuito
• simplificação de um circuito a partir de uma tabela verdade

Vamos imaginar que temos uma tabela verdade com 3 variáveis a, b, c

a b c | f(a,b,c)

0 0 0 | 0

0 0 1 | 0

0 1 0 | 0

0 1 1 | 0

1 0 0 | 0

1 0 1 | 1

1 1 0 | 1

1 1 1 | 1

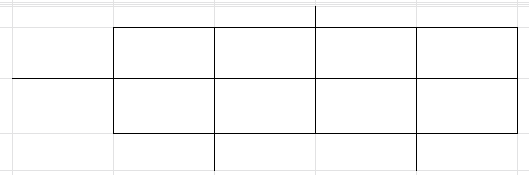
para começar adicionaremos um código cíclico na parte de cima com dois bits

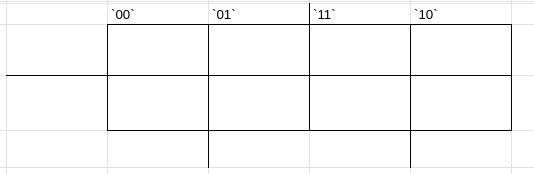
depois o valor 0 e 1 para o lado esquerdo

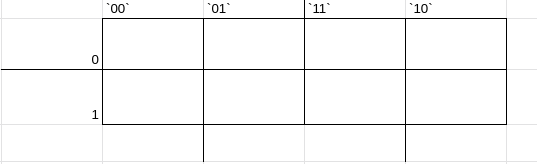
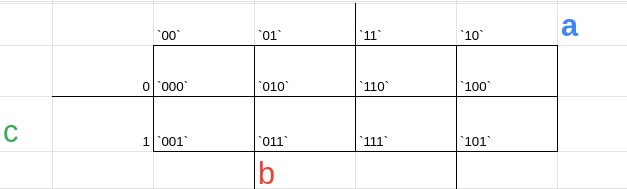
agora juntaremos a parte de cima com a do lado, lembrando que a de cima vem sempre primeiro, então, dessa forma, teremos:

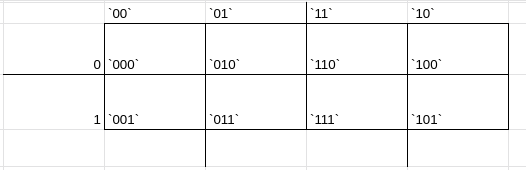
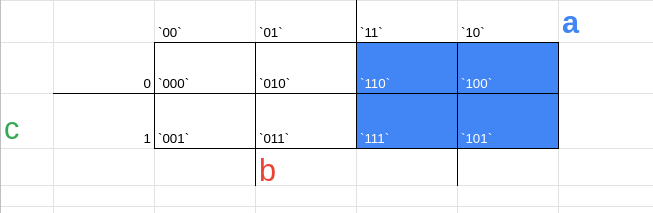
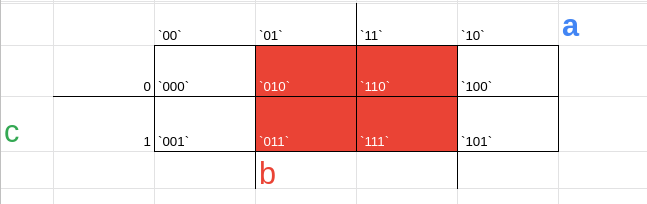
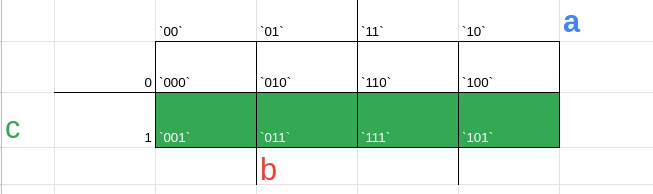
agora associaremos como região 'a' tudo aquilo que possui 1 no primeiro valor, como região b tudo aquilo que tem 1 no 'b' e região 'c' tudo que tem 1 no c

antes de continuar devemos saber o que significa vizinhança no mapa de karnaugh

vizinhança nada mais é do que os valores que estão em volta de uma certa célula

exemplo:

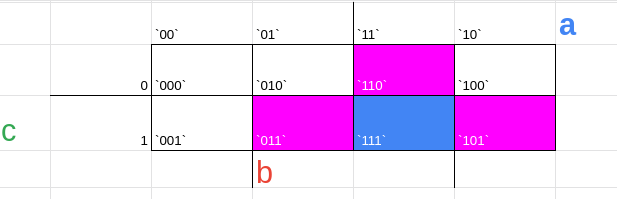
veja que tudo que está em rosa é vizinho de 111

repare também que a distância entre o valor 111 para os demais é sempre 1

distancia 111--110 → 1

distancia 111--011 → 1

distancia 111--101 → 1

sendo assim, no mapa de karnaugh todos os 3 vizinhos de um número possuem distância para ele de 1 e estarão sempre a sua volta, até mesmo do outro lado como no exemplo abaixo

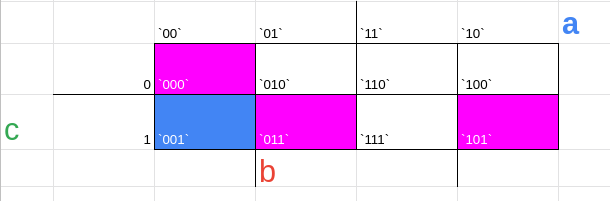
isso acontece pois, alem de seguir o padrão da distância 1, o mapa é pensando em 3 dimensões

continuando com a montagem

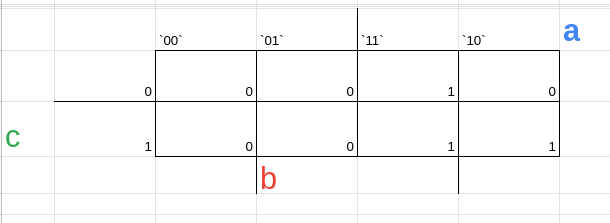
coloque nas células os valores correspondentes aos binários que cada célula continha com o valor da tabela verdade

agora você deve utilizar a regra do implicante primo

essa regra consiste em você pegar um fator de 2

nesse caso como temos os seguintes fatores de 2

2⁰ → 1

2¹ → 2

2² → 4

2³ → 8

ou seja podemos pegar até oito células de uma vez, já que temos 3 variáveis

e juntar células que possuem valores iguais sempre em quantidades desses fatores

obs: nesse caso pegaremos os valores 1

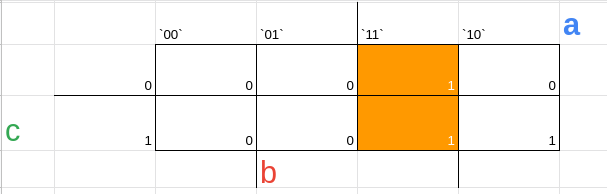
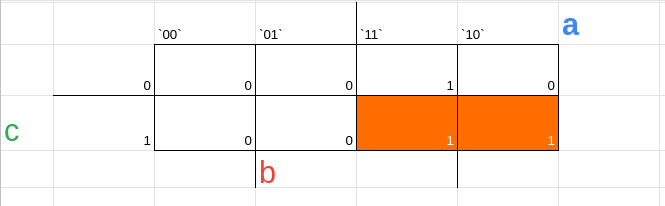
agora pegue esses dois implicantes e lembre de cada posição da tabela

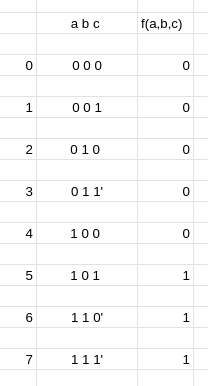
obs: ignore os ' que estão ali em a b c

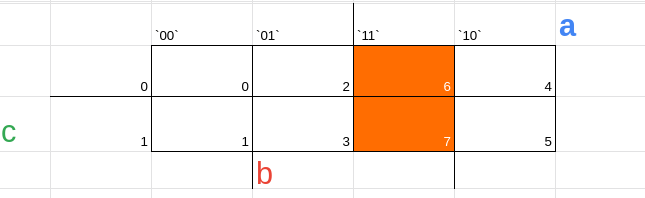
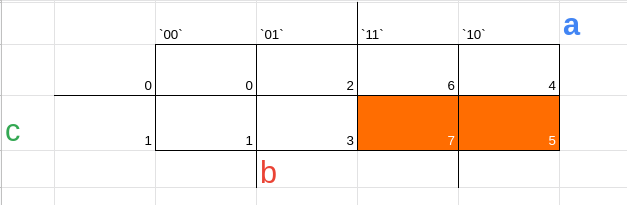
agora temos algo dessa forma

(6, 7) = a * b * c

(5,7) = a * b * c

obs: como pegamos apenas o valor 1 usamos a soma de produtos, caso contrário usaríamos o produto de somas

agora eliminaremos dessas expressões as variáveis em que sua região não contem o implicante inteiro

ficando dessa forma:

(6,7) = a * b

(5,7) = a * c

por fim, fazemos a soma dos produtos

f(a,b,c) = (a * b) + (a * c)

e caso você queira, você pode usar de novo os axiomas e simplificar

ficando:

f(a,b,c) = a(b * c)

repare que este foi o mesmo resultado que teríamos se fizéssemos com os axiomas

observações

as simplificações além de ajudarem a diminuir circuitos e expressões, também podem ser usadas na programação para diminuir expressões lógicas usadas em if e similares