Ciências da computação dia 3
coisas sobre matemática e alguns truques para fazer algumas contas mais rápido
Um pouco de história
- matemática era no principio considerada uma religião, já que o conhecimento era escasso e caro
- A partir do ano de 1500/1600 começaram a aparecer as primeiras gráficas que ajudaram a popularizar e baratear o conhecimento com livros e afins
Truques de matemática
multiplicação por 11 com 2 dígitos
25 * 11 = (primeiro numero)(primeiro + segundo numero)(segundo numero)
25 * 11 = 275
multiplicação de dois números iguais que terminam em 5
55 * 55 = (primeiro numero * sucessor)25
55 * 55 = 3025
Multiplicação decimais muito grandes
0.003 * 0.0004 * 0.0002 = x
multiplique os números 3 * 4 * 2
conte o numero de casas dps da vírgula somando de cada numero (3 casas no primeiro, 4 casas no segundo e 4 casas no terceiro, então 11 casas no total)
monte o numero
0, (numero d casas — as ocupadas pelo numero do final)(numero multiplicado no começo)
0,00000000024
raiz quadradas gigantes
√400000000
quando o numero sem ser 0 for um quadrado perfeito e o numero de zeros for par então
(raiz do primeiro)(numero de zeros /2)
20000
Curiosidades
Academus → herói grego que ajudava as pessoas em grandes negociações e grande negócios no geral, e toda vez que perguntavam o que devia ser feito para ele, ele dizia para ter algumas noites de sono para pensar
tomo → divisão
Dr. Helmont → Grande médico de 1660, médico do qual, fez uma receita de como germinar ratos, claramente essa receita não era algo real, pois apenas o que acontecia era uma mistura muito grande de coisas podres em um local úmido, do qual era propicio para ratos aparecerem e se aproveitarem dessa situação imunda. Não dizendo que ele era alguém burro ou algo do tipo, já que para a época era o conhecimento que eles tinham, tanto que até Newton acredito que era verdade a receita.
cada numero possui um numero de ângulos condizente com seu valor
o Z dos inteiros vem do matemático alemão Zahl que propôs esse conjunto
pi = circunferência de um cilindro / diâmetro da circunferência
phi
- número de ouro, número da beleza, número de Deus → 1,6261…
- Descoberto por Leonardo da Vinci (cara que fez a Monalisa e a primeira ideia sobre o helicóptero) 1550
- altura / dividido pela altura do umbigo ao chão = phi
- envergadura / distancia entre cotovelo e mão = phi
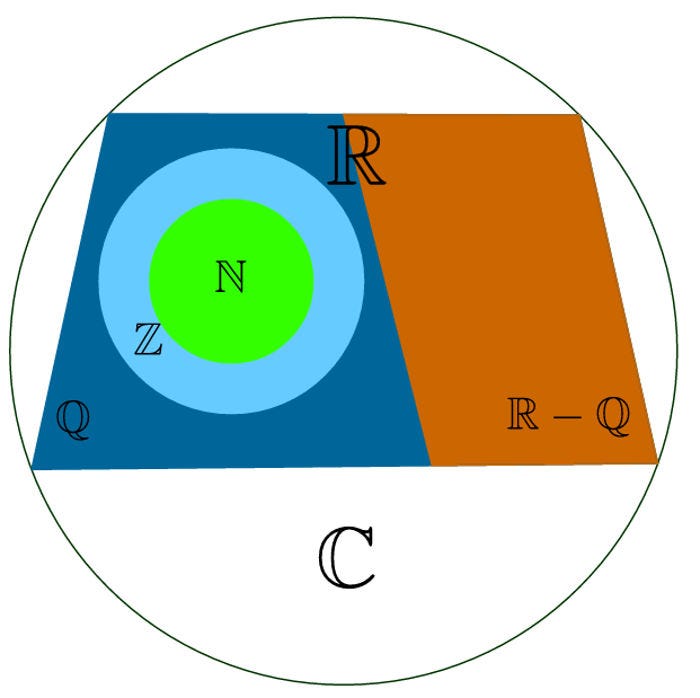
Conjuntos numéricos
Naturais →0, 1, 2, 3, 4, …
Inteiros → …, -2, -1, 0, 1, 2, …
Racionais → …, -0.5, -0.1232323, 0, 1, 1/2, 5, … (frações e dizimas entram aqui)
Irracionais → pi, 1.32313…, phi, … (números que você desconhece seu comportamento após a vírgula)
Dizimas periódicas
1,6262626262… → dizima simples (pois, após a vírgula o período já aparece)
1,654343434343… → dizima periódica composta (pois antes do período temos um numero diferente chamado de anti período)
resolver dizimas
do primeiro numero até o primeiro período — primeiro numero antes do período / um nove para cada numero do período e um zero para cada anti período
ex:
1,262626…
126–1 / 99 → 125/99
1,25434343…
12345–125 / 9900 → 12220/9900
Fração geratriz
frações que geram dizimas e decimais
0.5 → 1/2 ou 5/10
1,2626… → 125/99
0.3 → 3/10