Ciências da computação dia 266
Grafos
Graus (d)
- grau de um vértice → número de arestas incidentes a ele
- grau do grafo(grau máximo) → maior grau dos vertices
- grau de vertices isolados é 0 (também chamado só de isolado)
- d(v) = 1 → chamado de pendente, folha ou terminal
- menor grau do grafo é chamado de grau mínimo e é representado por δ(G)
- maior grau de um grafo é chamado de grau máximo e é representado por Δ(G)
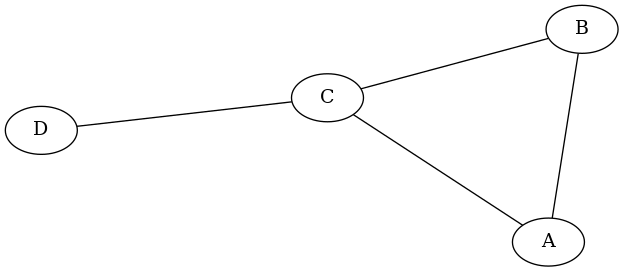
nesse exemplo, Δ(G) = 3 e δ(G)=1
- para grafos direcionados, temos graus de entrada e saída
- graus de entrada(din)→ quantas arestas estão entrando no vértice
- graus de saía(dout) → quantas arestas saem do vértice
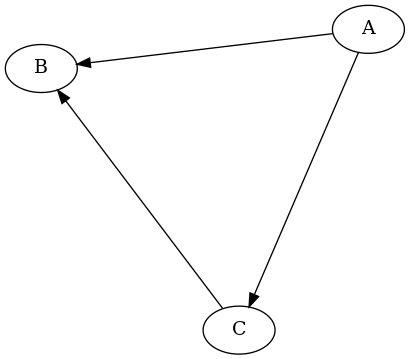
nesse caso, din(B) = 2 e dout(B) = 0
Problema de Königsberg
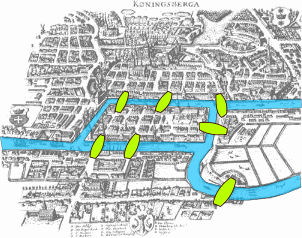
- problema que deu origem aos grafos
- problema das sete pontes
- passar por todas as pontes sem repetir nenhuma e voltar para o ponto inicial
Grafos
- por padrão um grafo não é direcionado
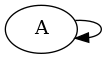
- para grafos não direcionados, um loop conta-se como duas arestas
- para grafos não direcionados com self-loop, conta-se como um multi-grafo (d(A) = 2)
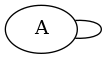
- em multi-grafos, dizemos que cada aresta é paralela
- a ordem de um grafo é o número de vértices que ele possui
- em grafos direcionados, um self-loop representa um vértice de entrada e um de saída