Ciências da computação dia 252

• um grafo pode ser composto de subgrafos
• há a possibilidade de um grafo não ter arestas
• grafos podem ter loops
• como o grafo é, depende do contexto
• grau de um vértice → quantas arestas saem dele

Problema das pontes

No problema das pontes, há quatro regiões, e 7 pontes que as interligam. A ideia aqui é descobrir se há alguma maneira de sair de um ponto, passar por todas as pontes, sem repetir nenhuma, e voltar ao ponto inicial.

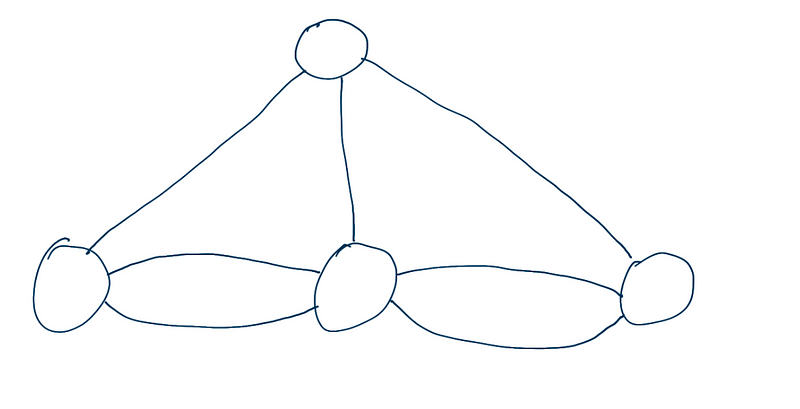
esse problema, pode ser visto como um grafo não dirigido, possuindo 4 vertices.

Nesse caso, para encontrar a solução, podemos olhar para o grau de cada nó.

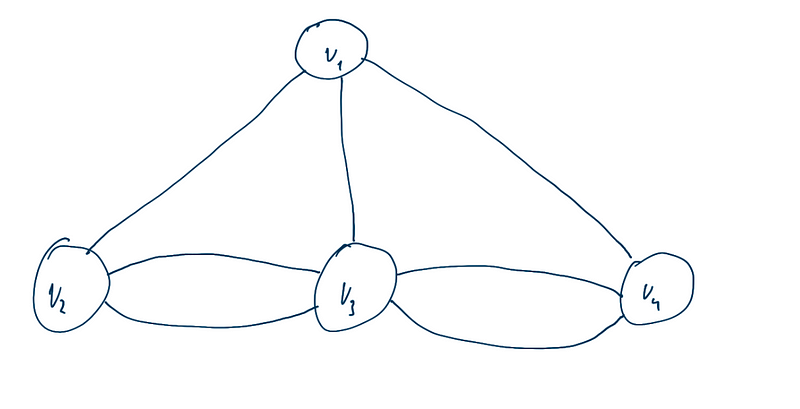
d(V1) = 3

d(V2) = 3

d(V3) = 5

d(V4) = 3

Pensando que, para sair de um local, e voltar para ele sem repetir o trajeto, precisamos de um numero par de caminhos, esse problema não é possível, já que todos os trajetos são ímpar.

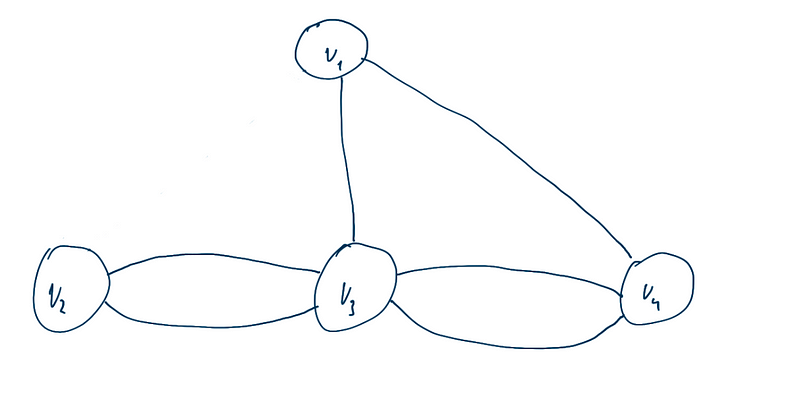
Mesmo reduzindo o numero de pontes, e deixando alguns graus pares, isso não será possível ainda.

Problema do tabuleiro

Imagine um tabuleiro 3x3 com quatro peças, duas nomeadas como A e duas como B. Todas estão nos cantos de uma certa forma. Aqui, queremos saber se é possível deixar essas peças no canto, deixando seus relativos lado a lado (pode ser tanto horizontal como vertical) movendo as apenas em L.

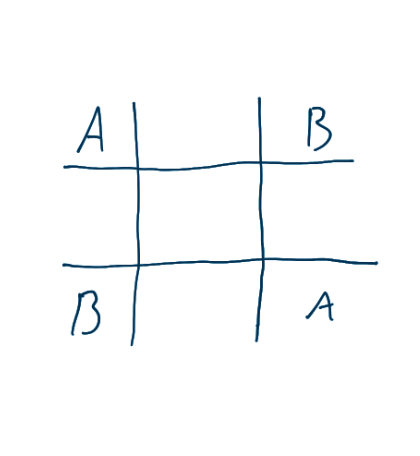
algo que poderíamos fazer é mapear as posições que cada posição do tabuleiro pode ir.

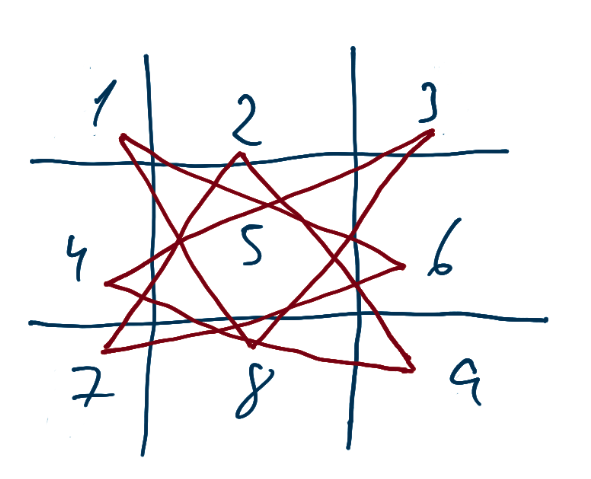
agora, podemos fazer um grafo com essas informações, para entender melhor o problema, será utilizado o layout circular.

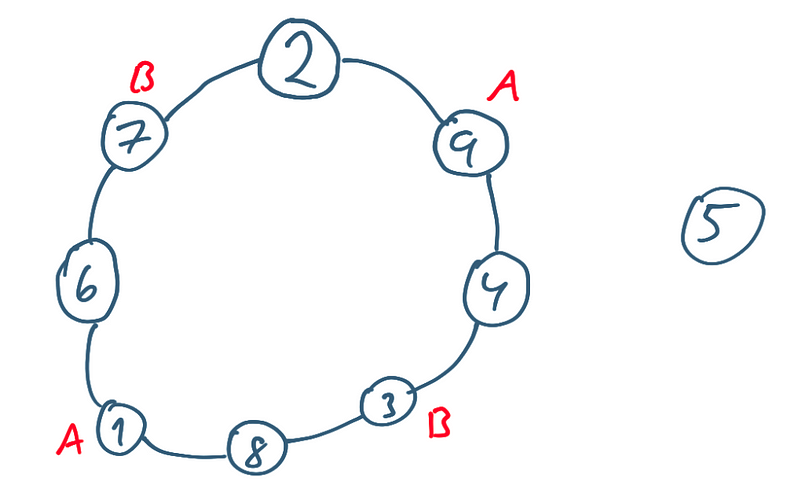
Observando o grafo do problema, é possível ver que, mesmo movimentando as peças para a esquerda ou direita, é impossível conseguir inverter as posições de A e B, sendo assim, é impossível fazer o que problema requer.