Ciências da computação dia 250

• tabela de distribuição de frequência → tabela estatísticas relativas a frequência dos valores na amostra (intervalo [ [ )

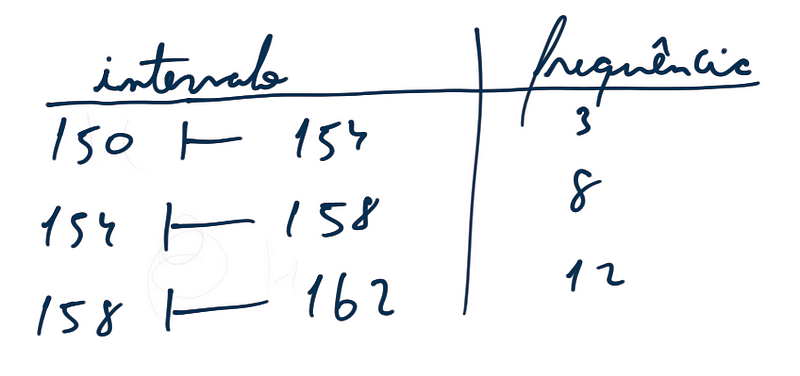
• classe(i) → intervalos
• limite inferior(li) → de cada intervalo, esse é o menor valor(150, 154, 158)
• limite superior(Li) → de cada intervalo, esse é o maior valor(154, 158, 162)
• amplitude(h) → tamanho do limite (Li --- li)
• Limite minimo(Lmin) → menor limite inferior(150)
• Limite máximo(Lmax) → maior limite superior (162)
• amplitude total (AT) → AT=Lmax-Lmin
• maior valor da amostra (Xmax)
• menor valor da amostra (Xmin)
• amplitude amostral (AA) → AA = Xmax --- Xmin
• ponto médio da classe (Xi) → média dos valores (valores da amostra)
• frequência absoluta(fi) → quantidade de aparições de um elemento contido em certo intervalo
• frequência relativa(fri) → fi/ Σfi
• frequência relativa % (fri%) → fri*100
• frequência acumulada (fac) → frequência absoluta da classe atual, somado com a frequência acumulada anterior

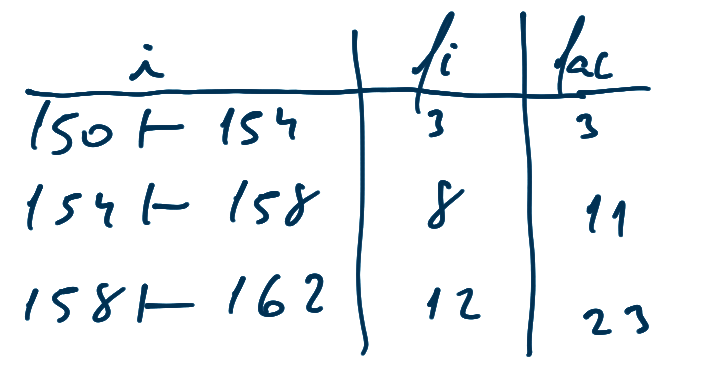
• frequência acumulada relativa(far) → fac/Σfi

Calculo do numero de intervalos

• depende do caso e da experiencia do pesquisador
• há algumas formulas que ajudam a achar também
• Critério da raiz → i = √n (i é o numero de intervalos e n a quantidade de elementos)
• formula de Sturges → i≅1 + 3.3*log(n)
• usando essas formulas, o valor não seria sempre exato, sendo assim, você pode ajustar colocando um a mais ou a menos, dependendo do caso
• para saber qual será a amplitude de cada intervalo, basta pegar o i resultante e fazer:

h = AA/i

• caso h seja muito pequeno, não vale a pena usar intervalos, as vezes utilizar os valores absolutos da amostra seja o melhor. Isso vai depender, novamente, da finalidade da pesquisa