Ciências da computação dia 25

Álgebra Booleana

• criada por George Boole
• a partir dos conceitos de conjunto vazio(0) e conjunto universo(1) ele criou essa álgebra
• possui 3 operações básicas → AND, OR, NOT
• No começo ela era usada apenas na filosofia, com proposições lógicas(século 18), mas com o advento dos semicondutores ela passou a ser usada também na eletrônica(a partir do século 20)

Ordem de precedência

NOT → AND → OR

POSTULADOS FUNDAMENTAIS

• seguindo esses postulados se prova que a álgebra booleana é válida

axioma 1(fechamento)

qualquer valor operado consigo mesmo resulta nele

x + x = x (OR)

x * x = x (AND)

A partir disso podemos simplificar o circuito, ao invés de utilizarmos uma porta para esse circuito, como sabemos que sempre a saída será igual a entrada, podemos simplesmente remover a porta e deixar apenas um fio

axioma 2 (elemento nulo)

valor que quando usado em uma certa operação o resultado sempre será ele

0 + 1 = 1 (valor nulo OR → 1)

1 * 0 = 0 (valor nulo AND → 0)

nesse podemos substituir as portas por apenas fios ou se necessário um pull up para o valor 1, e pull down para o valor 0

axioma 3 (elemento neutro)

valor que não modifica o resultado da operação

0 + 1 =1 (valor neutro OR → 0)

0 * 1 = 0 (valor neutro AND → 1)

nesse caso podemos também remover a porta e deixar apenas a entrada com um simples fio

axioma 4 (propriedade comutativa)

a ordem dos fatores não altera o produto

x + y = y + x

x * y = y * x

Infelizmente nesse caso o circuito não pode ser reduzido

axioma 5(propriedade associativa)

em operações iguais não importa por qual par você comece operando

x + y + z = (x + y) + z = x + (y+z) = y + (z + x)

x * y *z = (x * y) *z = x *(y*z) = y *(z *x)

Infelizmente nesse caso o circuito também não pode ser reduzido

axioma 6 (elemento inverso)

valor operado com seu valor inverso é sempre fixo

x + x' = 1

x * x' = 0

nesse caso você pode trocar isso por um pull up ou pull down, ou só um fio

axioma 7 (propriedade distributiva)

você pode fazer distributiva entre os valores

x * (y + z) = x * y + x * z

x +(y * z) = (x + y) * (x + z)

também não há como reduzir

expressão dual

uma expressão dual é basicamente o inverso de uma expressão

exemplo

(x + y) * (a + 0) + c ← expressão comum a

(x * y) + (a + 1) * c ← expressão dual a'

para fazer uma expressão dual, pegue a expressão e inversa AND com OR e OR com AND e inverta também 0 com 1 e 1 com 0

Circuitos melhores

para se fazer um circuito melhor deve ser levado em consideração o tempo que ele levará para entregar o resultado, para isso pegue cada circuito (cada coluna de componentes) e adicione 10ns para cada, o circuito que tiver menos tempo de execução será um pouco melhor para executar uma certa tarefa

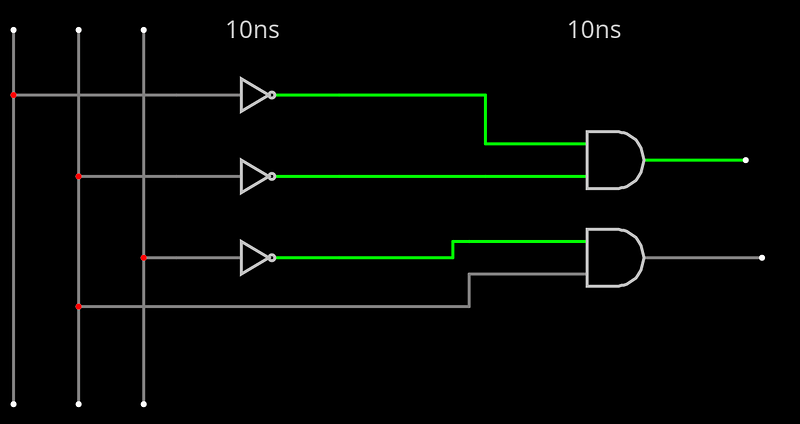
nesse caso o tempo total de um circuito será de 20ns

OBSERVAÇÕES

• número de bits de um processador significa o quanto de bits ele pode processar de uma só vez