Ciências da computação dia 210

Análise sintática

• segunda fase da compilação
• usa gramática livre de contexto (por permitir recursões e outras coisas)
• dada uma gramática G e uma sentença S, o analisador identifica se S ∈ G
• recebe a lista de tokens da primeira fase

Métodos de derivação

• a esquerda → faz a substituição do simbolo não terminal a partir do lado esquerdo
• a direita → faz a substituição do simbolo não terminal a partir do lado direito

# a esquerda

S -> S * S
S -> a * S
S -> a * a

# a direita

S -> S * S
S -> S * a
S -> a * a

• pode ser visto em formato de árvore (AST (arvore sintatica abstrata)) ou parse tree

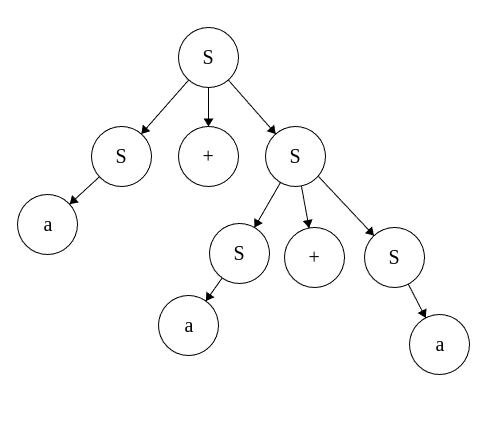
AST

• símbolos não terminais criam os ramos da árvore
• símbolos terminais são as folhas
• raiz é o símbolo inicial
• niveis mais baixos da árvore determinam qual a ordem de prescedencia das operaçoes (de baixo para cima)
• deve seguir todo o código fonte sem dar erros antes de analisar tudo
• apresenta a hierarquia de S

Ambiguidade

• gramática não pode ser ambígua
• gera duas ASTs para a mesma sentença

exemplo:

S -> if b then S
S -> if b then S else S
S -> a

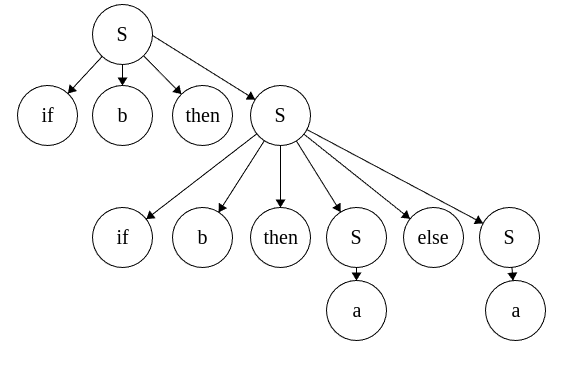
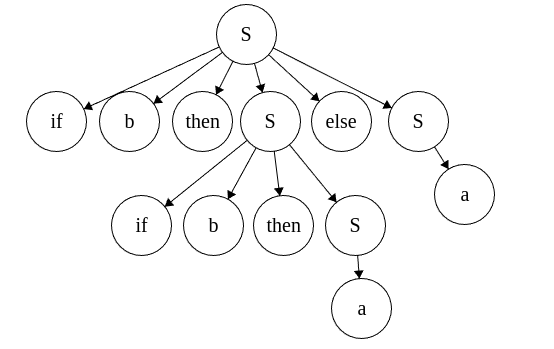
Nesse exemplo, um else pode ser associado a mais de um if, gerando incongrências

• não há algoritmo pré-pronto para determinar se uma gramática é ou não ambígua
• uma das maneiras de checar se uma gramática é ambigua é derivando à esquerda e a direita e verificar se há incongruências com as ordens de prescedencia
• regras que não definem ordem de prescedencia são ambiguas
• algumas das maneiras de remover a ambiguidade é adioncando novos símbolos não terminais

exemplo:

S -> S + S | a  (ambiguo pois não define ordem)


# sem ambiguidade
S -> S + T | T
T -> a


----

S -> S + S | S * S | T


E -> E + T | T
T -> T * F | F
F -> a

nessa versão sem ambiguidade é possivel ver que o operador * fica nos niveis 
mais baixos da AST, fazendo com que a ordem de prescedencia seja seguida

Alguns passos para remover a ambiguidade:

1. estabelecer a prescedencia os operadores
2. definir a associatividade dos operadores
3. usar a recursão à esquerda para força a associatividade à esquerda

Recursividade à esquerda

• acontece em gramáticas livre de contexto
• regra possui seu próprio símbolo como o símbolo mais à esquerda

Exemplo

A -> Aa | b

dessa forma, podemos ter uma sentença enorme que segue o padrão
baaaaaaaaaaaaaaaaaaaaaaaaaaaaaa..., contudo a àrvore cresce a esquerda indo:

Aa 
Aaa
Aaaa
Aaaaa
Aaaaaa
Aaaaaaa
baaaaaa

o que queremos é remover isso e fazer se tornar

bA
baA
baaA
baaaA
baaaa



para isso podemos fazer:

A -> bA' | b
A' -> aA' | a

Restrições gramaticais

• não pode haver U -> U
• não pode haver regras que não são usadas
• simbolo U deve permitir que a cadeia chegue à um símbolo terminal