Ciências da computação dia 206

Uma gramatica é composta de uma tupla com 4 items:

G = N, Σ, P, S

onde G é a gramática, N são os símbolos não terminais, Σ o alfabeto (simbolos terminais), P são as regras de derivação e S o símbolo inicial.

os símbolos terminais são aqueles que não possuem qualquer derivação, já os simbolos não terminais são aqueles que podem ser derivados para outros símbolos (ex: A(não terminal)-> b(terminal))

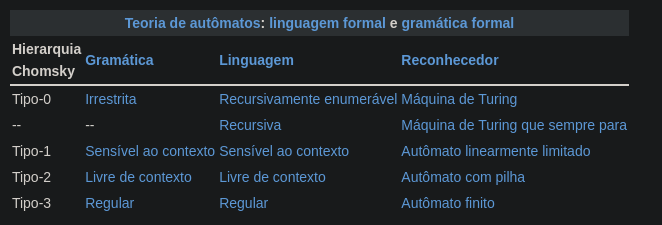
Segundo a hierarquia de Chomsky, temos a organização dos tipos de gramática elencados do mais díficil para o mais simples de reconhecer. Dentro dessas gramáticas temos as seguintes características.

Gramática Irrestrita

• não existe regra de produção
• linguagem natural
• impraticavel para linguagens de programação, já que possui muitos valores possíveis e nenhuma regra simples de seguir
• qualquer conjuntos de símbolos terminais e não terminais é válido
• a -> X, X -> a (qualquer simbolo pode gerar outro)
• apenas o operador vazio precisa ser definido X -> Ɛ

Gramática sensível ao contexto

• αAβ -> αyβ ,onde αβ são simbolos terminais e não terminais, A é um simbolo não terminal e y um símbolo terminal
• S -> Ɛ
• Como αβ podem ter qualquer combinação de dois símbolos, é possível ter inumeras combinações, fazendo com que essa gramática seja difícil de computar, sendo assim, impraticável

Gramática livre de contexto

• A -> α, S -> Ɛ

Gramática regular

• A -> a, A -> aβ, A-> βa
• linguagem lógica
• boa para linguagens de programação
• sempre do lado esquerdo há um símbolo não terminal
• as regras podem criar outras regras através da derivação
• na derivação um símbolo não terminal do lado direito pode ser substituido por um de uma regra que ele está do lado esquerdo

P = S -> aB, B -> cS, S -> Ɛ

S -> aB -> cS -> Ɛ

sendo assim A -> β

• S -> b1, S -> b2, S -> b3 = S -> b1|b2|b3

Exemplo

G = Vn, Vt, P, S

Vn = T, X

Vt = a,b

P = (T->aX), (T->Ɛ), (X->bT)

S = T

com isso, conseguimos derivar imediatamente de T, após cada aplicação de X -> bT a palavra ababab.

Nesse caso, pode ser visto que, utilizando as regras temos a seguinte linguagem:

L(G) = Ɛ, ab, abab, ababab, abababab, ...