Ciências da computação dia 193

Derivada

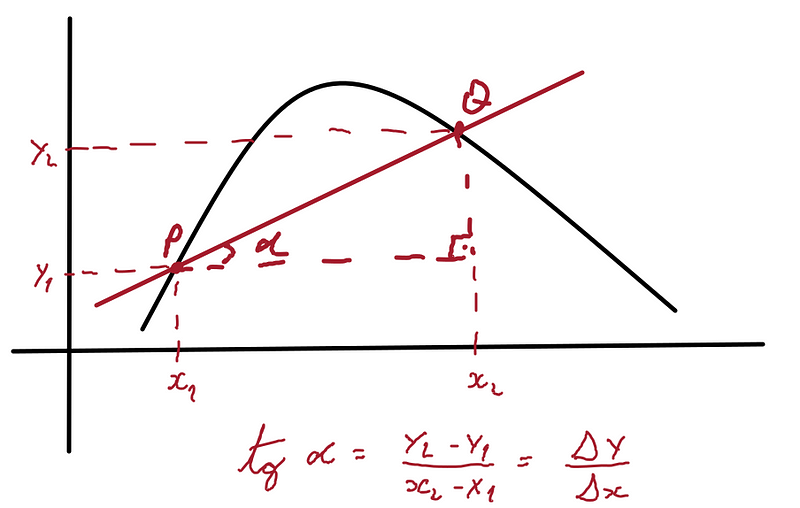
Se fizermos uma curva e passarmos uma linha secante (que toca apenas dois pontos) com os pontos P e Q nessa curva, teremos um triângulo retângulo. Com isso, podemos descobrir a tangente desse angulo, usando as coordenadas x e y relativos aos pontos P e Q.

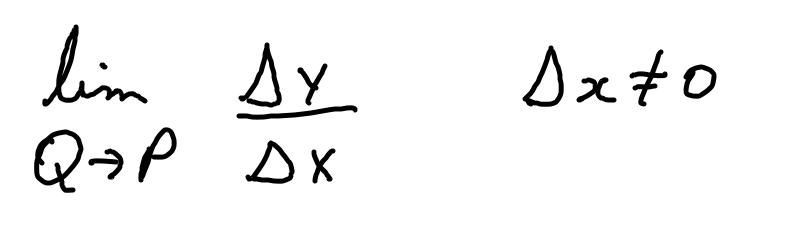
para encontrarmos então a reta tangente(reta que encosta em apenas um ponto), podemos aproximar o ponto Q do ponto P. Com isso, a razão cada vez mais se aproxima da indefinição 0/0.

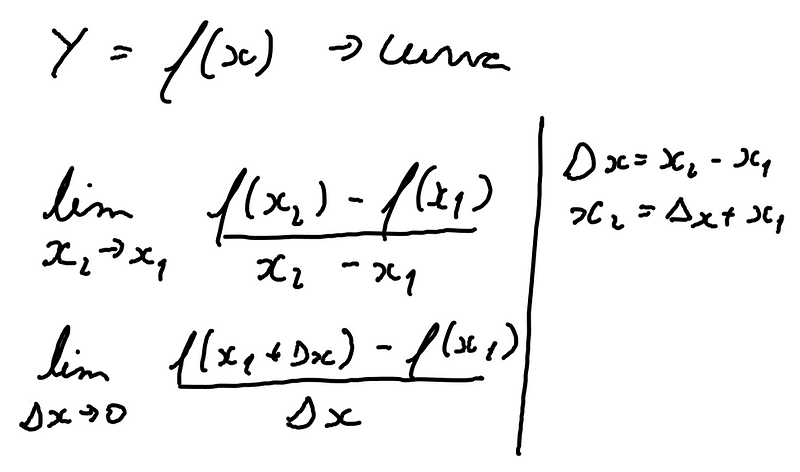
podemos fazer algumas modificações algébricas e chegar nessa equação final, sendo essa a definição de derivada em um ponto.

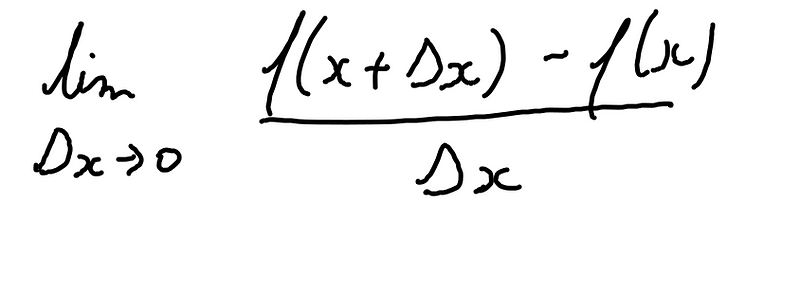
trocando x1 por x, definimos então a derivada de uma função.

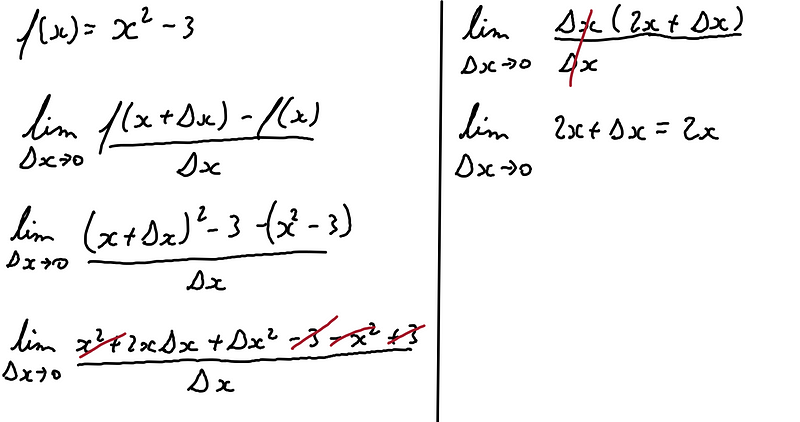
usando a definição, podemos pegar certas funções e deriva-lás.

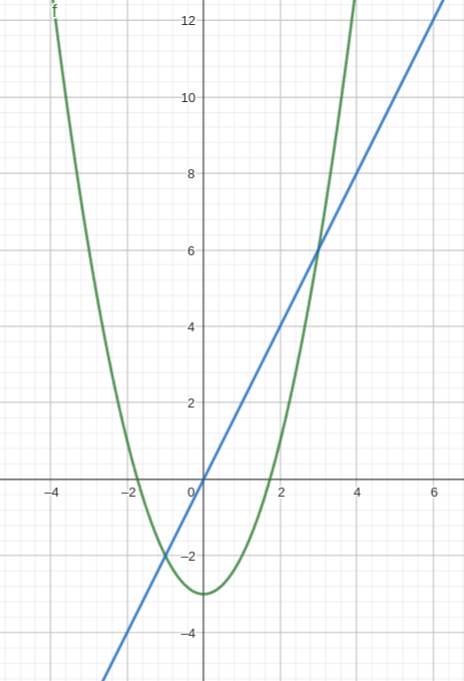
Retas

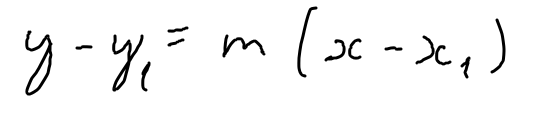
como o resultado da derivada nos da a inclinação (m) da reta tangente. Podemos pegar esses valores em um certo ponto (x1,y1) e descobrir a equação da reta tangente, lembrando que cada ponto da curva dará um (m) diferente, sendo necessário ir aproximando para valores melhores.

Física

Na física, as derivadas são extremamente úteis.

podemos começar vendo a função que descreve a posição de um corpo em determinados momentos.

A partir dessa função, podemos derivar e encontrar a função da velocidade.

Derivando a velocidade podemos encontrar a aceleração, e assim sucessivamente.

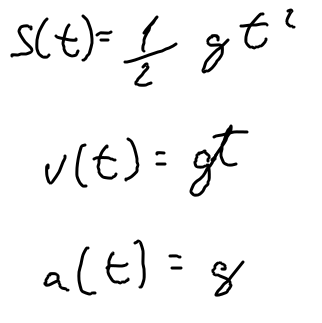
podemos também entender a função de um corpo em queda livre. Primeiro começamos com a função espaço, novamente, ao derivar conseguimos a velocidade, dada pela gravidade*tempo. Por fim conseguimos a aceleração que é a própria gravidade, demonstrando então que o faz um corpo em queda livre aumentar sua velocidade é a gravidade.