Ciências da computação dia 184
Arquitetura de computadores --- memoria em série
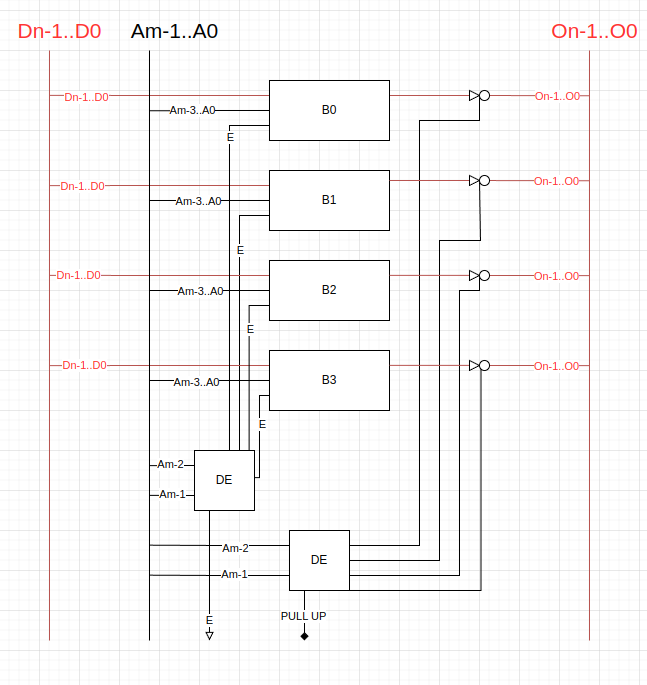
No exemplo acima, temos uma memoria genérica em série.
Nesse exemplo, temos 4 bancos de memória (B0-B3), 3 barramentos (dados (D), endereços(A) e saída de dados(O)), além de elementos como DE (decodificador de endereços), e os componentes (parecidos com uma porta not) ligados ao bus de saída, representando buffers com um trigger.
Nesse circuito, podemos setar o valor que queremos no barramento de dados, podemos configurar o endereço que o dado vai ser guardado no barramento de endereços. Ao darmos pulsos no clock(do qual foi omitido aqui), os dados passarão para os componentes, e quando ativarmos o E(enable, para escrita), o decodificador de endereços usará uma logica interna para determinar quais bancos serão necessários para guardar os dados, fazendo com que dados diferentes fiquem em endereços diferentes, fazendo então com que tenhamos mais endereços para guardar dados do que em circuitos paralelo).
Após guardar o dado, podemos colocar novamente o endereço que queremos ler, e o segundo DE se encarregará de verificar quais são os bancos necessários e assim acionar o trigger dos buffers para a passagem dos dados para o barramento de saída.
Nesse exemplo, é possível ver que os endereços dos bancos vão de Am-3 até A0, enquanto o barramento em si vai de Am-1 até A0, isso acontece pois os 2 bits mais significativos são usados para identificar o banco usado (como no caso aqui estamos usando 4 bancos(2²) dois bits é o suficiente).
Se quiséssemos, por exemplo, uma memoria de 1Kb, poderíamos usar a memoria base de 256x8, então 4*256 = 1024 = 1Kb, sendo assim, o total de bits para endereçar 1Kb é 2¹⁰, ou seja A9..A0. (repare que 256 = 2⁸ ou seja A7..A0, novamente os dois bits entram em ação).
Para ver melhor como os endereços são distribuídos entre os bancos, podemos pegar o exemplo de 1Kb e identificar o range de valores da seguinte forma:
B0 → 0000000000--0011111111
B1 → 0100000000--0111111111
B2 → 1000000000--1011111111
B3 → 1100000000--1111111111
Repare que a cada iteração é feito +1 com os dois primeiros bits, indicando então qual o banco será usado para determinado valor.
Com isso podemos entender porque o DE utiliza os dois bits mais significativos.