Ciências da computação dia 10

agora para sistemas lineares, equações irracionais e equações biquadradas.

Sistemas lineares

• duas equações que se correlacionam e possuem mais de uma incógnita.

para resolver sistemas lineares um dos métodos apresentados foi o método da adição, para utilizá-lo, pegue os números que acompanham x e multiplique a parte de cima pelo número de x de baixo e o de baixo pelo de cima, lembrando que um desses dois deve ser transformado em negativo, após isso pegue as equações que resultaram e some as, lembrando que os valores de x ao serem somados devem resultar em 0, o resultado dessa soma será uma equação do primeiro grau simples de resolver. após resolver e encontrar o Y com isso, pegue qualquer uma das equações anteriores e substitua o Y.

Equações irracionais

• equações que apresentam uma incógnita dentro de uma raiz

Para resolver elas você pode usar uma artimanha, você eleva os dois lados da equação pelo índice da raiz, dessa forma você poderá cancelar a raiz e continuar a equação, você pode usar essa artimanha quantas vezes forem necessárias.

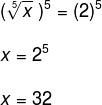
Equações biquadradas

• equações que possuem um valor do quarto grau

Para resolver essas equações indique uma letra para ser = x², a partir dai você pode substituir o valor que esta elevado a quatro pela letra que você indicou ao, já que (x²)² = x⁴, e o x² da equação por essa letra, iguale a equação a 0, e pronto você tem uma equação do segundo grau. Realizando a fórmula de Bhaskara, você encontrará duas respostas, agora para encontrar os valores corretos faça a raiz quadrada de cada um desses valores, já que a letra que você indicou = x², então a √letra que você indicou = x, dessa forma você encontrará 4 respostas, isso pois para cada raiz quadrada que você fizer para as raízes encontradas pela fórmula de Bhaskara você terá um valor positivo e um negativo ou seja ±a raiz.